The BSD conjecture is true for most elliptic curves

This past weekend I had the privilege to speak at the Southern California Number Theory Day along with Manjul Bhargava, Elena Fuchs, and Chris Skinner.  Manjul and Chris spoke about a series of remarkable results which, when combined, prove that at least 66.48% of elliptic curves over \mathbf Q satisfy the (rank part of the) Birch and Swinnerton-Dyer (BSD) Conjecture (and have finite Shafarevich-Tate group).  Bhargava’s work with Arul Shankar also proves that at least 20.6% of elliptic curves over \mathbf Q have rank 0, at least 83.75% have rank at most 1, and the average rank is at most 0.885.  Conjecturally, 50% of elliptic curves have rank 0, 50% have rank 1, and 0% have rank bigger than 1, and thus the average rank should be 0.5.  (And conjecturally, 100% of elliptic curves satisfy the BSD conjecture. :))  Before the work of Bhargava-Shankar and Bhargava-Skinner (which makes use of recent results of Skinner-Urban. Wei Zhang, and the Dokchitser brothers among others), the best known unconditional results in this direction were that at least 0% of elliptic curves have rank 0, at least 0% have rank 1, the average rank is at most infinity, and at least 0% of curves satisfy the BSD conjecture.

I will attempt to briefly summarize some of the main ideas from their talks; see these papers by Bhargava-Skinner and Bhargava-Shankar for more details and references.  (The paper of Bhargava, Skinner, and Wei Zhang showing 66.48% is forthcoming. [Note added 7/8/14: that paper has now appeared at http://arxiv.org/abs/1407.1826.])

An elliptic curve over \mathbf Q has a unique minimal representation as E_{A,B}: y^2 = x^3 + Ax + B with A, B \in {\mathbf Z} and \Delta := -4A^3 - 27B^2 \neq 0 (where minimal means that if p^4 \mid A then p^6 \nmid B for all primes p).   The so-called naive height of E_{A,B} is defined by H(E_{A,B}) = {\rm max}(4|A^3|,27B^2).   It is easy to see that the number of elliptic curves E_{A,B} with H(E_{A,B}) \leq X grows asymptotically like a constant times X^{5/6}.  If we order elliptic curves by height, it makes sense to ask what is the average rank, what is the average size of the n-Selmer group for some n, what percentage of elliptic curves satisfy the BSD conjecture, etc.; moreover, standard conjectures predict that if we order elliptic curves by discriminant or conductor then the answers to these questions would not change.  The only known method to bound the average rank is to bound the average size of the n-Selmer group for some n.  Conjecturally (see for example this paper), the average size of the n-Selmer group is \sigma(n) (the sum of the divisors of n) for all n.  Bhargava and Shankar have now proved this conjecture for n \leq 5, with n=5 being the hardest and most recent case.  Because of the hypotheses in the work of Skinner-Urban, the case n=5 was crucial for obtaining the results mentioned above.

Here is a very quick and impressionistic outline of how Bhargava and Shankar obtain these results.  The basic idea is to represent n-Selmer elements geometrically and then to parametrize those geometric objects as the (integral) orbits of some algebraic group acting on a vector space; one then constructs a fundamental domain for the group action and counts the number of lattice points in the fundamental domain using techniques from Minkowski and Siegel’s geometry of numbers.  (One also needs a “geometric sieve” to count the number of lattice points which satisfy the local conditions required to be an n-Selmer element and not just an element of H^1({\mathbf Q},E[n]).)

More concretely, for each n \leq 5 Bhargava and Shankar construct a representation V of an algebraic group G defined over {\mathbf Z} such that:

(a) The ring of invariants of G({\mathbf C}) acting on V({\mathbf C}) is freely generated by two elements A and B.

(b) There is an injective map {\rm Sel}_n(E_{A,B}) \rightarrowtail G({\mathbf Z}) which is “compatible” with the A and B on both sides.

For example, when n=2 one takes V to be the space of binary quartic forms with the natural action of G = {\rm SL_2}; this way of representing 2-Selmer elements goes back to the work of Birch and Swinnerton-Dyer (and is in fact underlies the computations they did in discovering their celebrated conjecture).  And for n=3, one takes V to be the space of ternary cubic forms with the natural action of G={\rm SL_3}.  The case n=5 is quite a bit more subtle, and I won’t describe it here, but it goes back to classical work of Cayley representing genus 1 curves in {\mathbf P}^4 as the (non-complete) intersection of five quadrics defined by the 4 \times 4 sub-Pfaffians of a 5 \times 5 skew-symmetric matrix of linear forms; see this paper for more details.  (It is unknown whether such a parametrization of n-Selmer elements exists for any n > 5, but if one could implement the Bhargava-Shankar method for an infinite sequence of n, it would prove that 100% of elliptic curves over Q satisfy BSD and that the average rank is the expected value 1/2.)  Note that one needs to work out the invariant theory over {\mathbf Z} and not just over the complex numbers, which requires a lot of non-classical work.

Importantly, thanks to the geometric sieve, the above program can be carried out not just for the family of all E_{A,B} but also for families defined by (an infinite number of) congruence conditions on A and B; this is crucial when combining the work of Bhargava-Shankar with the results of Skinner-Urban-Zhang because the latter results involve various technical hypotheses on the elliptic curves in question but one can show that these hypotheses are satisfied on average in certain sub-families defined by congruence conditions.

That was a quick summary of Bhargava’s talk; now I’ll give an even quicker summary of Chris Skinner’s talk.

Let p be a prime.  From the fundamental exact sequence 0 \to E({\mathbf Q})/p E({\mathbf Q}) \to {\rm Sel}_p(E) \to {\rm Sha}(E)[p] \to 0, one sees that if {\rm Sel}_p(E) = 0 then E has rank 0 and the BSD conjecture predicts that L(E,1) \neq 0..  Moreover, since {\rm Sha}(E) is conjecturally a finite group whose order (by properties of the Cassels-Tate pairing) is a perfect square, if {\rm Sel}_p(E) \cong {\mathbf Z}/p{\mathbf Z} and E has no rational p-torsion then E has rank 1 and the BSD conjecture predicts that L(E,s) vanishes to order 1 at s=1.  What Skinner and his collaborators have managed to prove is that these predictions hold if one assumes some additional hypotheses, and Bhargava-Skinner show that most elliptic curves satisfy these hypotheses!

For example, the rank 0 case is contained in the following result:

Theorem: Suppose p \geq 3 and that (a) E has good ordinary or multiplicative reduction at p; (b) E[p] is an irreducible representation; (c) there exists a prime \ell \neq p of multiplicative reduction such that E[p] is ramified at \ell; and (d) {\rm Sel}_p(E) = 0.  Then the algebraic and analytic rank of E are both zero.

The main ingredient in the proof of this result is the Iwasawa-Greenberg Main Conjecture proven by Skinner and Urban.

In the rank 1 case there are two similar results which I won’t state precisely here.  Importantly, though, these results assume that p \geq 5 and this is why the recent work of Bhargava-Shankar on the average size of 5-Selmer groups is crucial.  One of the new ingredients in the work of Skinner et. al. is a method to show, assuming  that {\rm Sel}_p(E) \cong {\mathbf Z}/p{\mathbf Z} and E has no rational p-torsion (plus a few more technical hypotheses), that a suitable Heegner point has infinite order.  Classically this is done using the Gross-Zagier formula but here one is not assuming that L(E,s) vanishes to order 1 so there is no obvious way to compute the height of the point.  So instead one uses a formula due to Bertolini-Darmon-Prasanna which relates the formal logarithm of the Heegner point to a special value of a suitable p-adic L-function.  The Main Conjecture and other results from Iwasawa theory are used to show that this p-adic L-value is nonzero and therefore the Heegner point has infinite order.

For those readers who know more about the subject than I do, please feel free to add details or insightful remarks in the comments section!

This entry was posted in Elliptic curves and tagged , , , . Bookmark the permalink.

4 thoughts on “The BSD conjecture is true for most elliptic curves”

  1. In his lecture Skinner remarked that the results he spoke about have a chance of working when p is a supersingular prime for E as well, and there is ongoing work with others to achieve that. When that happens, Bhargava said that a combination of all the different results will show that the rank part of BSD holds for over 80% of elliptic curves over Q.

    Reply

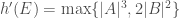  2. While the math is great, I think the use of percentages in some of these talks is a little silly. The notion of height that is employed in these papers is something like h(E) = \max\{|A|^3,|B|^2\}. However, if one instead used the minor variant h'(E) = \max\{|A|^3,2 |B|^2\}, then the percentages occurring as upper bounds would change! (Of course, in either case, one would still expect that the number of rank zero and rank one curves is 50%, and a “non-zero” percentage will remain so for any similar height.) The obsession with using percentages always seemed to me to be a quirky aspect of Manjul’s expositional style. The results concerning the average ranks of Selmer groups, on the other hand, are much more robust as far as variations of heights go. The emphasis percentages in these talks is a little like serving up a rare fillet mignon with ketchup — completely unnecessary!

    Reply

  3. Pingback: Noble lies at dinner parties | Mathematics without Apologies, by Michael Harris

Leave a comment