Next week I start a new position as Associate Dean for Faculty Development in the Georgia Tech College of Sciences. One of the things I’m looking forward to is getting to know more faculty outside the School of Mathematics and learning about their research. My knowledge of biology, in particular, is rather woeful, but I love reading about the latest developments in Quanta Magazine and elsewhere.
The other day I took my 14-year-old daughter, who is hoping to study genetics, to visit the lab of a Georgia Tech colleague in the School of Biology. During the visit we discussed how expensive it can be not just to purchase but also to maintain certain kinds of lab equipment, for example centrifuges. This reminded me about a blog post I’ve been meaning to write for a long time now…
Back in 2011-12, I spent a year as a faculty member at UC Berkeley and I became friends with some biologists there. One weekend afternoon I was chatting with a cancer researcher named Iswar Hariharan at a barbecue, and when he heard that I was a number theorist he told me about a problem he had been thinking about on and off for more than 15 years. The problem concerns balancing centrifuges.
A crash course on centrifuges
A centrifuge, as you probably know, is a laboratory device used to separate fluids based on density. The separation is achieved through centrifugal force by spinning a collection of test tubes at high speeds. As Iswar explained to me, it’s very important to balance a centrifuge before operating it; running a centrifuge with an unbalanced load can permanently damage it. A centrifuge is called balanced if the center of mass of the collection of test tubes coincides with the center of mass of the centrifuge itself. For example, here is balanced configuration of 8 test tubes in a 20-hole centrifuge:

There are also configurations of test tubes which are balanced, but less obviously so, such as this one with 13 test tubes and 24 holes:

If you spend a lot of time balancing centrifuges and have a mathematically curious mind, the following question might naturally arise:
Problem: For which pairs (n,k) with 1 ≤ k ≤ n can you find a way to balance k identical test tubes in an n-hole centrifuge?
This is precisely the question which Iswar started to think about, and in 1998 he arrived at a conjectural answer. Before I tell you Iswar’s conjecture (which he described to me at the barbecue), let’s think about a few special cases to get a feeling for the problem.
Some special cases
If n=3 then you can only balance the centrifuge if k=3, and if n=4 you can balance for k=2 and k=4.
If n=6, then it’s easy to see that you cannot balance the centrifuge if k=1 or 5 but you can if k=2,3,4, or 6:
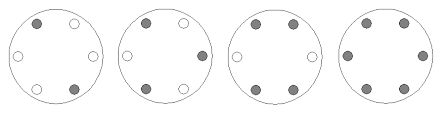
If n=5 or 7, on the other hand, you can only balance the centrifuge if k=n.
It seems that the answer might have something to do with whether or not n is prime… Let’s look at some more examples.
If n=8, then you can balance the centrifuge if and only if k is even.
If n=9, you can balance for k=3,6, or 9.
If n=10, you can balance for k= 2,4,5,6,8 or 10. Notice, for example, that if you wanted to balance the centrifuge with k=7, you could try to start with a balanced set of 5 test tubes (occupying every other slot) and then add two more in opposite holes, but there’s a problem: one out of each pair of opposite holes is already occupied! We will call this the overlap problem. It is in some sense the key subtlety in this problem.
If n=11, you can balance if and only if k=11.
If n=12, you can balance the centrifuge as long as k is not 1 or 11.
For a larger example: if n=21, you can balance if and only if k=3,6,7,9,12,14,15,18, or 21. For another illustration of the overlap problem, consider what happens when k=10. You could try to take a balanced configuration of 7 test tubes (spaced every 3) and then add 3 more in the shape of an equilateral triangle, but you will find that it doesn’t work because of that damned overlap problem.
If you stare long enough at this data, and at similar data for other values of n, you might come up with the same guess which Iswar made. I’ll give you a chance to stop and think about it before the spoiler which follows…
Iswar’s conjecture
Conjecture: You can balance k identical test tubes, 1 ≤ k ≤ n, in an n-hole centrifuge if and only if both k and n-k can be expressed as a sum of prime divisors of n.
For example, when n=21 and k=6 we have 6=3+3 and 21-6=15=3+3+3+3+3, and indeed the pair (21,6) can be balanced. But when k=10, although 10=3+7 there is no way to express n-k=11 as a combination of 3’s and 7’s. And the pair (21,10) cannot be balanced.
The conjecture predicts, for example, that if 6 divides n then every pair (n,k) with can be balanced (and when
this happens only if 6 divides n). This is presumably why the number of chambers in most commercial centrifuges is a multiple of 6.
A solution to the problem
When I left the barbecue, I started thinking about Iswar’s conjecture and it occurred to me that a natural way to phrase the question mathematically was in terms of roots of unity. In this language, the conjecture becomes:
Conjecture (alternate form): For any integers n ≥ 2 and 1 ≤ k ≤ n, one may find k distinct
roots of unity whose sum is 0 if and only if both k and n − k are expressible as linear combinations of prime factors of n with nonnegative coefficients.
I worked out some special cases of the conjecture from this perspective; for example, if n=p is prime then the conjecture says that only k=n should be balanced, and this follows from the fact that the cyclotomic polynomial is irreducible. But I couldn’t see how to deal with the general case. However, I knew there were some papers in the literature about linear relations between roots of unity (for example, Mann’s theorem), so I decided to do a Google search. And lo and behold, I found that Iswar’s conjecture had been proved in 2010 in this paper by Gary Sivek! I don’t think I would have found this reference if I hadn’t first translated the question into a problem about linear relations between roots of unity.
Sivek’s proof of the “if” direction is short and elementary. For the “only if” direction, he uses a theorem of Lam and Leung, who proved the analogous result but where the k roots of unity are not assumed to be distinct. The proof of Lam and Leung is based on a careful study of the kernel of the natural homomorphism (sending z to ) from the group ring
, where
is a cyclic group of order n, to the cyclotomic ring
.
I emailed Iswar telling him that the conjecture he had made back in 1998 was in fact correct, and he replied:
I am both happy and sad to get this email. On the one hand I am happy that I “guessed” the solution correctly (15 years ago). I am sad that I never acquired the mathematical skills to prove it myself!It is funny how our minds get stuck on some problems over multiple decades.Thanks for taking our conversation seriously.
Although it’s ultimately just a stimulating curiosity, and nothing which is going to cure cancer, I still think of this episode as a nice illustration of the intellectual cross-fertilization that can take place when scientists from different disciplines get together, whether at a research conference or a barbecue. I hope that I’m able to encourage and foster such interdisciplinary friendships in my new role in the College of Sciences. We’re off to a great start in 2018 in this regard with the new Southeast Center for Mathematics and Biology headquartered at Georgia Tech.
Concluding remarks
(1) Sivek, who it seems received his Ph.D. in mathematics from Berkeley in 2010, begins his paper by saying that his motivation came from the balanced centrifuge problem. I would conjecture that the problem came to him indirectly through Iswar, but I don’t know for sure.
(2) It would be interesting to know for which k there is a unique way (up to rotational symmetry) to balance the pair (n,k). Or more generally, exactly r ways (for some fixed positive integer r).
(3) There is in fact a relationship between this problem and something I’ve been thinking about recently in my own research. I’m currently interested in “matroids over partial hyperstructures” such as partial fields and, more generally, tracts. (This post is not the place to explain such things, but see this guest blog post which I wrote for the Matroid Union for details.) If n is an even positive integer, the balanced centrifuge problem is equivalent to deciding for which k there is a k-term relation in the nullset of the tract associated to the partial field
, where
is the group of
roots of unity in
.
Ahh, so a centrifuge is just like a Hilbert space. Got it.
You’ve been reading up.
I think in my work i consider a continuous Version of this problem:
Click to access 1902.10824.pdf
Unfortunately this work containes the cumbersome parameters C. In the follow up work for the 3D case the diagonal lengths appear much more natural. I will replace that on arXive in the future. I think any closed configuartion, you can also see it as vectors attached at the origin that cancel out ecah other. So it can be seen as a distribution of mass on a centrifuge that will wil balance it.
Best wishes
Gerhard
By the way, I like your vids.
There are fun higher dimensional analogues.
There is a sequence of polyhedra which begin with a dodecahedron and whose limiting shape is an icosahedron and these can be projected to a sphere.
there’s the 120-cell, again to be projected on the three sphere, as well as the other polychora in R4.
there’s the polytope associated with E8, again to be projected onto a sphere.
There are hyperboloids crossed by rulings which are Lorenz invariant.
there’s the Klein quartic. eek?
symmetry with respect to more complicated discrete subgroups of SO(n,R) feels like it might have a representation theoretic flavor
This is totally awesome! Please come back to my lab every week.
Would you care to expand this problem to include hanging baskets? The scenario here would be to find the balanced solutions for (b,n,k) where b is the number of baskets with n holes each.
The hanging basket version of the problem is a really cool suggestion – thanks!
They should build centrifuges in characteristic 2. Then, for example, there would be solutions for n=7 and k=3,4. But, seriously, one can consider the problem in characteristic p>0 as well. Is the answer known there?
It’s a good question! As far as I know, a precise analogue of the results I mentioned is still open in characteristic p>0. However, Lam and Leung have partial results (on the “non-centrifuge” version of the question which allows roots of unity to be repeated) in their paper https://arxiv.org/pdf/math/9605216.pdf
Interesting article. I got here through a video that was made about this problem on YouTube. https://www.youtube.com/watch?v=7DHE8RnsCQ8
Same!
There is another parallel story about this problem.
I felt into it when I was a master’s student, when at some point I had to study determinants of circulant matrices modulo k. I rapidly realized that this problem can be linked to the one about barycenter on roots of unity. I only needed to solve the prime number case, which can be solved directly in the matrix world (or equivalently, as you say, by irreducibility of cyclotomic polynomials), but I found the problem quite funny and proposed it for the international tournament of young mathematicians: it appeared as problem n°5 in the 2012 edition:
https://docs.google.com/viewer?a=v&pid=sites&srcid=aXR5bS5vcmd8d3d3fGd4OjJlYmQwNDlkNGFhNzliZDA
I wasn’t aware of the fact that this problem had already been solved at this time. I felt on your blog post only by chance, so glad to know about it!
Nice story, thanks for sharing!
This centrifuge problem seems related to problem 1299 solved in Math Magazine 62 (1989) pp. 201-202. Thanks for such a good blog. – Daniel Shapiro
I found this an enjoyable read. I would have liked an explanation for why the assortment of tubes in the 13-tube 24-hole is balanced, as it does not appear to be so.
An ancillary question can be raised: Are there any combinations of tubes/slots that could not be balanced in two spinnings? That is, if you had 7 tubes in 12 slots, you could do it in a batch of 3 and a batch of 4. (We will, as all mathematicians do, accept that the obvious solution set of using a tube filled with water to balance as not valid.)
Hello, I am writing to you to ask a question about the proof of the 2010 theorem, the link to which you gave. The last step there is the induction transition for (p – 1)(q − 1) ≤ k < n/2. I would be very grateful if you would explain further reasoning. I tried to write with this question to the author's email, but for some reason it turned out to be invalid.
Here’s a slightly modified version of Sivek’s argument in this case which might make more sense to you. Suppose that . Then
. Then  with
with  and
and  , and one checks easily that
, and one checks easily that  . By the Pigeonhole Principle (or Sivek's lemma about concentric discs), if
. By the Pigeonhole Principle (or Sivek's lemma about concentric discs), if 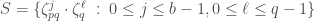 , there are at least
, there are at least 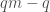 distinct sets
distinct sets 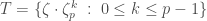 with
with 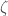 an
an 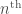 root of unity such that
root of unity such that  . Choosing
. Choosing  such sets
such sets 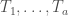 and adding together all the roots of unity in
and adding together all the roots of unity in  gives
gives 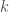 distinct
distinct 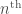 roots of unity whose sum is 0.
roots of unity whose sum is 0.
Pingback: Roots of Unity and Expressing numbers as linear combinations of primes – Math Solution
If you have $n$ links $(a_1, dots, a_n)$ that are connected by revolute joints then all angles that satisfy the equationbegin{align}sum_{j=1}^{n-1} a_j begin{pmatrix} cos(alpha_j) sin(alpha_j)end{pmatrix} = begin{pmatrix} a_n 0end{pmatrix}end{align}define a closed configuration. Here link $a_n$ is supposed to lie on the positive $x-$axis and one of its ends coincides with the origin. If you think of the vectors in the equation above as being attached to the origin a closed configuration can also be interpreted as a sum of forces that add up to zero, where the magnitude of the force is given by the length of the link. If you suppose that the little glass tubes on a centrifuge are placed at angle $alpha$ and are filled by different amounts of liquid a closed configuration can also be seen as a solution to a continues version of the balanced centrifuge problem. The space of closed configurations of planar linkages has also been investigated.