Circles, the Basel Problem, and the Apparent Brightness of Stars

On Pi Day 2016, I wrote in this post about the remarkable fact, discovered by Euler, that the probability that two randomly chosen integers have no prime factors in common is $\frac{6}{\pi^2}$ . The proof makes use of the famous identity $\sum_{n=1}^\infty \frac{1}{n^2} = \frac{\pi^2}{6}$ , often referred to as the “Basel problem”, which is also due to Euler. In the 2016 post I presented Euler’s original solution to the Basel problem using the Taylor series expansion for $\frac{\sin(x)}{x}$ .

In honor of Pi Day 2018, I’d like to explain a simple and intuitive solution to the Basel problem due to Johan Wästlund. (Wästlund’s paper is here; see also this YouTube video, which is where I first heard about this approach – thanks to Francis Su for sharing it on Facebook!) Wästlund’s approach is motivated by physical considerations (the inverse-square law which governs the apparent brightness of a light source) and uses only basic Euclidean geometry and trigonometry.

Outline of the proof

A brief outline of Wästlund’s argument is as follows:

Step 1: Through some simple algebraic manipulations, it suffices to prove the equivalent formula $\sum_{n=-\infty}^\infty \frac{1}{(n-\frac{1}{2})^2} = \pi^2$ . This, in turn, follows (setting $x = \frac{1}{2}$ ) from the following more general fact:

Theorem: For every real number $x$ which is not an integer, we have $\sum_{n=-\infty}^\infty \frac{1}{(n-x)^2} = \left(\frac{\pi}{\sin(\pi x)}\right)^2.$

Step 2: Let $N=2M$ be even, and think of $x$ (which without loss of generality we may suppose satisfies $0 < x \leq \frac{1}{2}$ ) as a point $P$ on the real number line. Place $N$ stars of equal brightness on the number line, with one star at each integer (i.e., “lattice”) point of the half-open interval $(-M,M]$ . Then by the inverse square law, we can interpret the partial sum $\sum_{n=-M}^M \frac{1}{(n-x)^2}$ as the total apparent brightness at $P$ of the $N$ -star system.

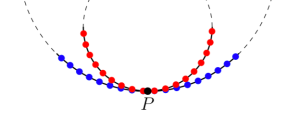
Step 3: We may approximate (to any desired precision) the $N$ lattice points of $(-M,M]$ by $N$ equally spaced points along the perimeter a circle of very large radius which is tangent to the real number line at $P$ . We can therefore replace our system of $N$ stars on a line by a system of $N$ stars lying on some arc centered at $P$ inside a large circle (like the blue dots in Figure 1).

Figure 1

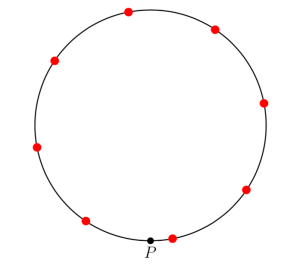
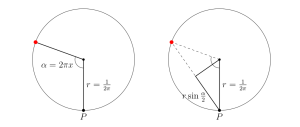
Step 4: Suppose we place $N$ equally spaced stars of equal brightness all the way around the perimeter of a circle of circumference $N$ , and measure the total apparent brightness $f_N(x)$ at some point $P$ on the circle having distance $x$ (measured along the circle) from the nearest star (see Figure 2).

Figure 2

Then the inverse square law implies that for $T=2N$ , “most” (in a precise quantitative sense) of this brightness comes from the $N$ stars closest to $P$ .

Step 5: Iterating this observation, let $g^{(N)}_k(x)$ denote the total apparent brightness of the $N$ closest stars to $P$ when we place $2^k N$ equally spaced stars around the perimeter of a circle of circumference $2^k N$ , with the closest star at arc-distance $x$ from $P$ (see Figure 1 again). Then $f_{2^k N}(x) = g^{(N)}_k(x) + o_N(1)$ .

Step 6: By an elegant geometric argument related to the “inverse Pythagoran theorem” (see Figure 3), it turns out that for every $N$ we have $f_N(x) = f_{2N}(x)$ . In other words, we can replace a system of $N$ equally spaced stars along a circle of circumference $N$ , tangent to the real line at $P$ , by a system of $2N$ equally spaced stars along a circle of circumference $2N$ , also tangent to the real line at $P$ , in such a way that the total apparent brightness at $P$ is unchanged.

Figure 3

This implies, by induction, that $f_{2^k N}(x) = f_N(x)$ for all natural numbers $k$ . Combining this with the previous step, we obtain $f_N(x) = g^{(N)}_k(x) + o_N(1)$ .

Step 7: In particular, if $N$ is itself a large power of 2, then $g^{(N)}_k(x)$ is approximately $f_N(x) = f_1(x)$ for all $k$ . When $k$ is also large, $g^{(N)}_k(x)$ is approximately $\sum_{n=-M}^M \frac{1}{(n-x)^2}$ (where as before $N=2M$ ). It follows that $\sum_{n=-\infty}^\infty \frac{1}{(n-x)^2} = f_1(x)$ .

Step 8: By elementary trigonometry, we have $f_1(x) = \left(\frac{\pi}{\sin(\pi x)}\right)^2$ , which proves the Theorem.

Some Euclidean geometry

The crucial, and most innovative, part of the argument is the fact from Step 6 that $f_N(x)=f_{2N}(x)$ . This is most easily explained for $N=1$ , though the proof in the general case is essentially the same. So let’s examine how Wästlund proves that $f_1(x) = f_2(x)$ .

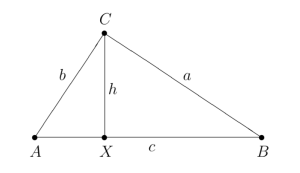
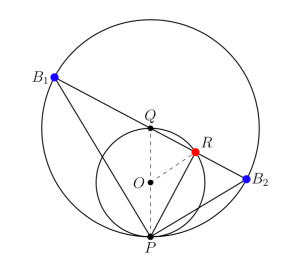
The argument is based on the “Inverse Pythagorean Theorem”, which is the assertion that in the setting of Figure 4 (where ACB is a right angle), we have $\frac{1}{a^2} + \frac{1}{b^2} = \frac{1}{h^2}$ .

Figure 4

It is an elementary exercise to deduce this from the usual Pythagorean Theorem.

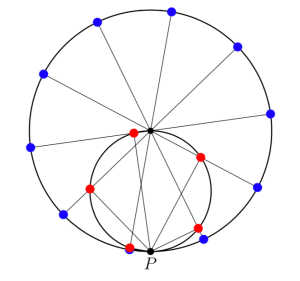
Given a single star (represented by the red point R in Figure 5) on a circle of radius 1, tangent to the real line at $P$ , we can replace it by two equally spaced stars (the blue points $B_1$ and $B_2$ ) on a circle of radius 2, also tangent to the real line at $P$ , in such a way that the apparent brightness of the red star at $P$ equals the sum of the apparent brightnesses of the two blue stars at $P$ .

Figure 5

The construction of $B_1$ and $B_2$ from $R$ goes as follows. Let $O$ be the center of the smaller circle, and let $Q$ be the center of the larger circle. Then $B_1$ and $B_2$ are the two points where the line $QR$ intersects the larger circle.

Since $PQ$ is a diameter of the smaller circle, $\angle PRQ$ is a right angle. The formula $f_1(x) = f_2(x)$ expressing the equality between the apparent brightness at $P$ in the red and blue star systems, will follow immediately from the Inverse Pythagorean theorem once we show that the (counterclockwise) arc-distance from $P$ to $R$ equals the (counterclockwise) arc-distance from $P$ to $B_2$ .

To see this, first note that $2\pi$ times the arc distance from $P$ to $R$ is equal to the measure (in radians) of the central angle $\angle POR$ . And $2\pi$ times the arc distance from $P$ to $B_2$ is equal to 2 (the circumference of the larger circle) times the measure of the central angle $\angle PQB_2$ . So it suffices to show that $\angle PQB_2 = \frac{1}{2} \angle POR$ . This follows from the fact that $\angle PQB_2 = \angle PQR$ , which intercepts the same arc of the small circle as the central angle $\angle POR$ .

By a similar argument, replacing each red star by two blue stars as in Figure 3 above, it follows that $f_N(x)=f_{2N}(x)$ for all $N$ .

The base case $N=1$ (Step 8)

In the base case $N=1$ , the quantity $f_1(x)$ is just $\frac{1}{d(P,Q)^2}$ where $C$ is a circle of circumference 1 (and hence radius $\frac{1}{2\pi}$ ), $P,Q$ are points on $C$ which are at distance $x$ as measured along the circumference of $C$ , and $d(P,Q)$ denotes the Euclidean (chordal) distance between $P$ and $Q$ . It is an elementary trigonometry exercise to show that $d(P,Q) = \frac{\sin(\pi x)}{\pi}$ (see Figure 6).

Figure 6

By induction on $k$ , we find:

Proposition 1: $f_N(x) = f_1(x) = \left(\frac{\pi}{\sin(\pi x)}\right)^2$ whenever $N=2^k$ is a power of 2.

The remaining technical details

We now show that when $N$ is large, $f_{2N}$ is approximately equal to $\sum_{n=-\infty}^\infty \frac{1}{(n-x)^2}$ .

Consider the $2N$ -star system along a circle of circumference $2N$ (and radius $r = \frac{N}{\pi}$ ). The total brightness at $P$ is, by definition, $f_{2N}(x)$ . Now remove the $N$ stars furthest from $P$ , and consider the total brightness $g(x)$ of the remaining $N$ stars. Since each of the $N$ deleted stars has distance at least $r\sqrt{2}$ from $P$ , it follows that $|f_{2N}(x) - g(x)| \leq N \cdot \frac{1}{(r\sqrt{2})^2} = \frac{\pi^2}{2N}$ .

By a similar argument, if we begin with the $2^k N$ -star system on a circle of radius $\frac{2^kN}{\pi}$ and remove all but the closest $N$ stars to $P$ , and denote by $g^{(N)}_k(x)$ the total brightness of the remaining $N$ stars, we have $|g^{(N)}_k(x) - g^{(N)}_{k-1}(x)| \leq \frac{\pi^2}{(2N)4^k}.$

On the other hand, it’s geometrically clear (since the radii of the circles approach infinity) that

$\lim_{k \to \infty} g^{(N)}_k(x) = \sum_{|n-x| < \frac{N}{2}} \frac{1}{(n-x)^2}.$

By the triangle inequality, the difference between $g^{(N)}_k(x)$ and $f_{2N}(x)$ is bounded by $\frac{\pi^2}{2N} (1 + \frac{1}{4} + \frac{1}{16} + \cdots) = \frac{2\pi^2}{3N}.$

Letting $k \to \infty$ gives, for any fixed $N$ , that

$\sum_{|n-x| < \frac{N}{2}} \frac{1}{(n-x)^2} = f_{2N}(x) + o_N(1).$

Taking $N$ to be an arbitrarily large power of 2 and applying Proposition 1 now yields Theorem 1 (in the special case $0 < x \leq \frac{1}{2}$ , but the general case follows easily from this).

Concluding Remarks

The above estimates can be used to prove a posteriori that $f_{N}(x) = \left(\frac{\pi}{\sin(\pi x)}\right)^2$ for all positive integers $N$ , not just powers of 2. This is reminiscent of Cauchy’s inductive proof of the inequality between the arithmetic mean and geometric mean which first establishes the result for powers of 2.
To get from Theorem 1 to Euler’s theorem that $S := \sum_{n=1}^\infty \frac{1}{n^2}$ is equal to $\frac{\pi^2}{6}$ , we can proceed as follows. First, setting $x=\frac{1}{2}$ in Theorem 1 gives $\sum_{n=-\infty}^\infty \frac{1}{(n-\frac{1}{2})^2} = \pi^2$ . Multiplying both sides of this equality by $\frac{1}{4}$ yields $2(1 + \frac{1}{3^2} + \frac{1}{5^2} + \cdots) = \frac{\pi^2}{4}.$ But $S - (1 + \frac{1}{3^2} + \frac{1}{5^2} + \cdots) = \frac{1}{4} S,$ and thus $S = \frac{4}{3} \cdot \frac{\pi^2}{8} = \frac{\pi^2}{6}$ as desired.
Alternatively, as pointed out to me by Keith Conrad, one can deduce $S = \frac{\pi^2}{6}$ from Theorem 1 as follows. Subtracting $\frac{1}{x^2}$ from both sides of the formula in Theorem 1 yields $\sum_{n=1}^\infty \left( \frac{1}{(x-n)^2} + \frac{1}{(x+n)^2} \right) = (\frac{\pi}{\sin \pi x})^2 - \frac{1}{x^2}.$ The Taylor series of the right-hand side around $x=0$ is $\frac{\pi^2}{3} + \frac{\pi^4}{15}x^2 + \cdots$ Setting $x=0$ gives $2 \sum_{n=1}^\infty \frac{1}{n^2} = \frac{\pi^2}{3}$ and thus $S = \frac{\pi^2}{6}$ . And differentiating both sides of $\sum_{n=1}^\infty \left( \frac{1}{(x-n)^2} + \frac{1}{(x+n)^2} \right) = \frac{\pi^2}{3} + \frac{\pi^4}{15}x^2 + \cdots$ twice and then setting $x=0$ gives $12 \sum_{n=1}^\infty \frac{1}{n^4} = \frac{2\pi^4}{15}$ and thus $\sum_{n=1}^\infty \frac{1}{n^4} = \frac{\pi^4}{90}.$ One gets, in a similar way, an explicit formula for $\sum_{n=1}^\infty \frac{1}{n^{2k}}$ for all positive integers $k$ .
It should hopefully be clear that the argument we’ve presented uses “physics” only for intuition; it is a rigorous mathematical proof.