Probability, Primes, and Pi

What is the probability that two randomly chosen integers have no prime factors in common? In honor of Pi Day, I’d like to explain the surprising answer: $6/\pi^2$ .

The hero of this story is Leonhard Euler, who worked out this astonishing connection between prime numbers and $\pi$ through a series of brilliant insights. In the spirit of Euler, I will be rather cavalier about issues of convergence and rigor here, focusing on the key underlying ideas.

Let the probability in question be denoted $P$ . Euler’s first observation is that if $a$ and $b$ are chosen at random, the probability that they are both even is $1/4$ , and so the probability that they are not both even is $1 - 1/4$ . Similarly, the probability that $a$ and $b$ are both divisible by 3 is $1/9$ , so the probability that they are not both divisible by 3 is $1 - 1/9$ . The probability that $a$ and $b$ are not both divisible by either 2 or 3 is therefore $(1-\frac{1}{4})(1-\frac{1}{9}).$ Continuing in this way, Euler finds that $P$ can be expressed as an infinite product over all primes:

$P = (1-\frac{1}{2^2})(1-\frac{1}{3^2})(1-\frac{1}{5^2})\cdots = \prod_{p {\rm \; prime}} (1 - \frac{1}{p^2}).$

Euler’s next step is to note that by the formula for the sum of a geometric series, $(1 - \frac{1}{p^2})^{-1} = 1 + \frac{1}{p^2} + \frac{1}{p^4} + \cdots$ and therefore we can rewrite our formula for $P$ as a formula for $1/P$ involving an infinite product of infinite sums:

$\frac{1}{P} = (1 + \frac{1}{2^2} + \frac{1}{2^4} + \cdots)(1 + \frac{1}{3^2} + \frac{1}{3^4} + \cdots)(1 + \frac{1}{5^2} + \frac{1}{5^4} + \cdots) \cdots$

Euler, in typically bold fashion, decides not to panic about all these infinities and just multiplies everything out term-by-term. He notices that the leading 1’s in each parenthetical expression multiply out to give 1, the $\frac{1}{2^2}$ together with all the other leading 1’s multiply out to give $\frac{1}{2^2}$ , and the $\frac{1}{3^2}$ together with all the other leading 1’s multiply out to give $\frac{1}{3^2}$ . In fact, Euler realizes that there is a unique way to obtain $\frac{1}{n^2}$ for each positive integer $n$ : use the prime factorization of $n$ to read off which terms to multiply together. For example, to obtain $\frac{1}{100^2}$ we choose $\frac{1}{2^4}$ from the first parenthetical expression, $\frac{1}{5^4}$ from the third, and 1’s from everywhere else. The terms which don’t involve choosing 1 all but finitely many times are neglible, according to Euler’s keen intuition (which is not hard to make precise with a bit of calculus that we’ll skip here). Therefore:

$\frac{1}{P} = \prod_{p {\rm \; prime}} (1 - \frac{1}{p^2})^{-1} = 1 + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \cdots = \sum_{n=1}^\infty \frac{1}{n^2}.$

Now calculating the value of the infinite sum $\sum_{n=1}^\infty \frac{1}{n^2}$ is a famous problem (often referred to as the Basel problem). Here’s how Euler solves it.

The Taylor series for $\sin(x)$ is

$\sin(x) = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots$

and therefore

$\frac{\sin(x)}{x} = 1 - \frac{x^2}{3!} + \frac{x^4}{5!} - \frac{x^6}{7!} + \cdots$

The roots of $\frac{\sin(x)}{x}$ are $x = \pm \pi, \pm 2\pi, \pm 3\pi, \ldots$ and so thinking of the Taylor series for $\frac{\sin(x)}{x}$ as an “infinite polynomial”, Euler obtains the identity

$1 - \frac{x^2}{3!} + \frac{x^4}{5!} - \frac{x^6}{7!} + \cdots = (1 - \frac{x}{\pi}) (1 + \frac{x}{\pi}) (1 - \frac{x}{2\pi}) (1 + \frac{x}{2\pi}) (1 - \frac{x}{3\pi}) (1 + \frac{x}{3\pi})\cdots$

Now the right-hand side can be simplified, using the difference of squares formula $(1+y)(1-y) = 1-y^2$ , as

$(1 - \frac{x^2}{\pi^2})(1 - \frac{x^2}{(2\pi)^2})(1 - \frac{x^2}{(3\pi)^2})\cdots = 1 - (\frac{1}{\pi^2} + \frac{1}{4\pi^2} + \frac{1}{9\pi^2} + \cdots) x^2 + (\cdots)x^4 + \cdots$

Comparing coefficients of $x^2$ in both sides of the identity

$1 - \frac{x^2}{3!} + \frac{x^4}{5!} - \frac{x^6}{7!} + \cdots = 1 - (\frac{1}{\pi^2} + \frac{1}{4\pi^2} + \frac{1}{9\pi^2} + \cdots) x^2 + (\cdots)x^4 + \cdots,$

Euler obtains $-\frac{1}{6} = -\frac{1}{\pi^2}(1 + \frac{1}{4} + \frac{1}{9} + \cdots),$ which can be rearranged to give $\sum_{n=1}^\infty \frac{1}{n^2} = \frac{\pi^2}{6}.$ Therefore $P = \frac{6}{\pi^2}$ as claimed.

Rest in peace, Euler. And happy Pi Day to the rest of you!

Concluding remarks:

Keith Conrad points out that there is something amiss with the above Pi Pie. Can you figure out what it is?
For a rigorous proof of the formula $\prod_{p {\rm \; prime}} (1 - \frac{1}{p^2})^{-1} = \sum_{n=1}^\infty \frac{1}{n^2},$ see for example Chapter 1 in these Trinity College lecture notes. To make the formula $\frac{\sin(x)}{x}= (1 - \frac{x}{\pi}) (1 + \frac{x}{\pi}) (1 - \frac{x}{2\pi}) (1 + \frac{x}{2\pi}) (1 - \frac{x}{3\pi}) (1 + \frac{x}{3\pi})\cdots$ rigorous, one can apply the Weierstrass Factorization Theorem.
For 13 other solutions to the Basel problem, see these notes by Robin Chapman.
For a more rigorous proof that $P = 6/\pi^2,$ see e.g. Theorem 8.1 of these lecture notes by Fabian Pazuki. (The definition of the Weil height function on projective space shows that $P = \frac{1}{2} \lim_{T \to \infty} \frac{{\mathcal N}({\mathbb P}^1({\mathbb Q}),T)}{T^2}$ , which by Theorem 8.1 of loc. cit. is $\frac{1}{2} a({\mathbb Q},1) = \frac{1}{\zeta(2)}.$ ) Note that this proof utilizes the Möbius inversion formula instead of Euler’s product formula $\prod_{p {\rm \; prime}} (1 - \frac{1}{p^2})^{-1} = \sum_{n=1}^\infty \frac{1}{n^2}.$

4 thoughts on “Probability, Primes, and Pi”

Antoine Chambert-Loir says:

April 15, 2016 at 7:19 pm

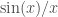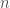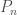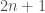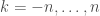There is a nice undergraduate proof of the formula for $\sin(x)/x$ that runs as follows: for every integer $n$ , write $\sin((2n+1)x)=P_n(\sin(x))$ , for some polynomial $P_n$ of degree $2n+1$ ; its roots are $\sin(k\pi/n)$ , for $k=-n,\dots,n$ , hence $\sin((2n+1)x)=c \sin(x)\prod_{k=1}^n(\sin^2(x)-\sin^2(k\pi/n))$ , for some constant $c$ , hence $\sin((2n+1)x)=(2n+1)\sin(x) \prod_{k=1}^n(1-\sin^2(x)/\sin^2(k\pi/n))$ . 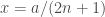Set $x=a/(2n+1)$ , one gets $\sin(a)/(2n+1)\sin(a/(2n+1))= \prod_{k=1}^n (1- \sin^2(a/(2n+1))/\sin^2(k\pi/n))$ . 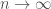Now let $n\to\infty$ , justifying the limit interchange via, e.g., dominated convergence.

- Matt Baker says:
  
  April 15, 2016 at 8:23 pm
  
  That’s a nice argument!
  
  - KC says:
    
    March 15, 2021 at 3:03 am
    
    That “nice undergraduate proof” is the way Koblitz works out the infinite product representation of $sin(\pi x)/(\pi x)$ for real $x$ in Chapter II of his $p$-adic analysis book.
Pingback: Circles, the Basel Problem, and the Apparent Brightness of Stars | Matt Baker's Math Blog