The Stern-Brocot tree, Hurwitz’s theorem, and the Markoff uniqueness conjecture

My goal in this post is to describe a surprising and beautiful method (the Stern-Brocot tree) for generating all positive reduced fractions. I’ll then discuss how properties of the tree yield a simple, direct proof of a famous result in Diophantine approximation due to Hurwitz. Finally, I’ll discuss how improvements to Hurwitz’s theorem led Markoff to define another tree with some mysterious (and partly conjectural) similarities to the Stern-Brocot tree.

The Stern-Brocot tree

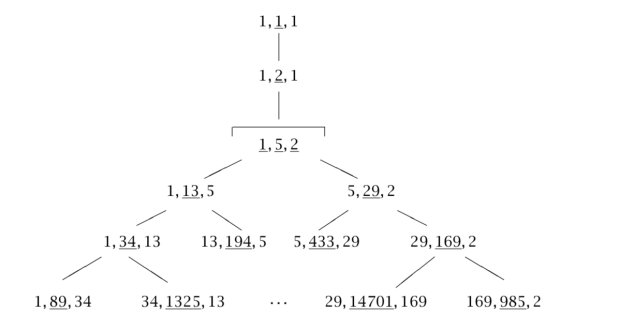
We first describe what I’ll christen the “extended Stern-Brocot tree” $\tilde{T}$ . It’s an ordered binary tree whose root note is labeled by the triple $(0,1,\infty)=(0/1, 1/1, 1/0)$ . Each node in the tree is labeled with an ordered triple of rational numbers (plus $\infty$ ), written in lowest terms, and each node has two children. If a node is labeled by the triple $(a,b,c)$ , then its left child is labeled $(a,a \vee b,b)$ and its right child is labeled $(b,b \vee c,c)$ , where $m/n \vee m'/n := (m+m')/(n+n')$ denotes the mediant of $m/n$ and $m'/n'$ . For example, the two children of the root $(0/1, 1/1, 1/0)$ are $(0/1, 1/2, 1/1)$ and $(1/1,2/1, 1/0)$ . And the two children of $(0/1, 1/2, 1/1)$ are $(0/1, 1/3, 1/2)$ and $(1/2,2/3, 1/1)$ . Here is a depiction of all descendents of $(0/1, 1/2, 1/1)$ in the extended Stern-Brocot tree:

A branch of the extended Stern-Brocot tree (from [1])

To get the Stern-Brocot tree $T$ , we keep just the mediants (the middle entry) and throw away the first and last entry in each triple:

The Stern-Brocot tree T (from [2]). The branch consisting of 1/2 and its descendants corresponds to the previous picture.

We can construct the Stern-Brocot tree T without reference to the extended tree by the following recursive rule: each fraction is the mediant of its closest ancestor to the left and its closest ancestor to the right, where a “left ancestor” of $\alpha$ is an ancestor which is less than $\alpha$ and a “right ancestor” is one which is greater than $\alpha$ .

The Stern-Brocot tree has a number of remarkable properties, the most notable of which is that every positive reduced fraction appears exactly once in the tree. Let’s see why this is the case…

Properties of the Stern-Brocot tree

We record the following properties of the Stern-Brocot and extended Stern-Brocot trees:

(a) Every triple $(a,b,c)$ occurring in $\tilde{T}$ has $a < b < c$ .

Proof: A simple calculation shows that the mediant of two distinct fractions $m/n$ and $m'/n'$ is always strictly between $m/n$ and $m'/n'$ .

(b) For every triple $(a,b,c)$ occurring in $\tilde{T}$ , we have $a \wedge b = b \wedge c = a \wedge c = -1$ , where $m/n \wedge m'/n' := mn' - m'n$ .

Proof: This holds for the root node, and a simple calculation shows that if it holds for a given node then it also holds for both children; the result follows by induction.

Proof: If $m/n, m',n'$ are reduced and $mn' - m'n = -1$ , then $n(m+m') - m(n+n') = 1$ and thus the GCD of $m+m'$ and $n+n'$ is 1. The result now follows from (b) by induction.

(d) Given $v,w \in T$ , let ${\rm inf}(v,w)$ be the least common ancestor of $v$ and $w$ . Then $v < w$ iff $v$ is a descendent of (or equal to) the left child of ${\rm inf}(v,w)$ and $w$ is a descendent of (or equal to) the right child of ${\rm inf}(v,w)$ .

Proof: Again, this is a straightforward induction.

(e) No fraction appears more than once in $T$ .

Proof: This follows immediately from (d).

(f) For every triple $(a,b,c)$ occurring in $\tilde{T}$ , $b$ has a smaller denominator than any other fraction between $a$ and $c$ .

Proof: Let $m'' / n''$ be any fraction between $a = m/n$ and $c = m' / n'$ . Then $1/n n' = m'/n' - m/n = (m'n'' - n'm'')/n'n'' + (m''n - n''m)/nn'' \geq (n+n'')/n n' n''.$

It follows that $n'' \geq n + n'$ , and the right-hand side is the denominator of $b$ . If equality holds, then $m'n'' - n'm'' = m''n - n''m = 1$ , which implies that $m'' = m+m'$ and $n''=n+n'$ .

(g) Every reduced positive fraction $s/t$ appears in $T$ .

Proof: (Sketch) Assume for simplicity that $s/t < 1$ (the general case is similar). We claim that $s/t$ appears at the latest in row $t$ of $T$ . Indeed, if $s/t$ has not already appeared by row $t-1$ , then there is a triple $(a,b,c)$ in row $t-1$ of $\tilde{T}$ with $a < s/t < c$ . By induction and the uniqueness part of (f), it follows that $b=s/t$ .

Combining (c), (e), and (g), we find:

Theorem: Every reduced fraction appears exactly once in $T.$

Stern-Brocot expansions of real numbers

Every positive real number $\alpha$ has a “Stern-Brocot expansion” consisting of a (possibly empty, possibly infinite) string of L’s and R’s determined by starting at the root and moving downwards through $\tilde{T}$ . At each stage, we move to the node labeled by unique triple $(a,b,c)$ with $\alpha \in (a,c)$ , stopping if $\alpha = b$ , and we record whether we went left or right in order to reach $(a,b,c)$ .

For example, the Stern-Brocot expansions of $5/7$ and $4/5$ are $LRRL$ and $LRRR$ , respectively. In this way, every positive rational number corresponds to a unique finite string (with 1 corresponding to the empty string), and every positive irrational number corresponds to a unique infinite string. The inverse-golden ratio $1/\phi = (-1 + \sqrt{5})/2$ corresponds to the infinite string $LRLRLRLR\cdots,$ and a result of Euler implies that the irrational number $e$ corresponds to the infinite string $RL^0RLR^2LRL^4RLR^6LRL^8R\cdots$

(If you’re familiar with continued fractions, there is a simple dictionary between Stern-Brocot and continued fraction expansions: a finite Stern-Brocot expansion of the form $R^{a_0}L^{a_1}R^{a_2}\cdots L^{a_{n-1}}$ or $R^{a_0}L^{a_1}R^{a_2}\cdots R^{a_{n-1}}$ with all $a_i \geq 0$ corresponds to the finite continued fraction $[a_0, a_1, a_2, \cdots, a_{n-1}, 1]$ , and an infinite Stern-Brocot expansion of the form $R^{a_0}L^{a_1}R^{a_2}\cdots$ corresponds to the infinite continued fraction $[a_0, a_1, a_2, \cdots ].$ )

Diophantine approximation

Given a real number $\alpha > 0$ , the Stern-Brocot triples corresponding to $\alpha$ are the triples $(a,b,c)$ appearing as vertices in the rooted path in $\tilde{T}$ which we just described. The mediants of these triples are called the semiconvergents of $\alpha$ . For example, when $\alpha = 5/7$ the corresponding Stern-Brocot triples are $(0,1,\infty), (0,1/2,1),(1/2,2/3,1),(2/3,3/4,1)$ , and $(2/3,5/7,3/4)$ , and the semiconvergents are $1, 1/2, 2/3, 3/4, 5/7$ .

For the inverse-golden ratio $1/\phi$ the semiconvergents are $1, 1/2, 2/3, 3/5, 5/8, 8/13,\ldots$ (ratios of consecutive Fibonacci numbers). The last semiconvergent of a rational number $\alpha$ is equal to $\alpha$ , and if $\alpha$ is irrational then the semiconvergents converge to $\alpha$ .

(The name semiconvergent comes from the fact that every convergent of the corresponding continued fraction is a semiconvergent, but not necessarily vice-versa.)

The most important fact about semiconvergents is that they give the closest approximations to $\alpha$ with a given denominator, i.e., a reduced fraction $m/n$ is a semiconvergent of $\alpha$ iff $m/n$ is closer to $\alpha$ than any other fraction of the form $m'/n'$ with $n' \leq n$ .

This leads us into the theory of Diophantine approximation, which is precisely concerned with such approximations by rational numbers. The cornerstone of this theory is Dirichlet’s Approximation Theorem, which is the following assertion:

Theorem (Dirichlet): If $\alpha$ is a positive irrational number, there are infinitely many reduced fractions $m/n$ with $|\alpha - \frac{m}{n}| \leq \frac{1}{n^2}.$

Remarks:

The “trivial” bound in Dirichlet’s theorem would be $\frac{1}{n}$ , since for every positive integer $n$ there is a rational number $m/n$ with $|\alpha - \frac{m}{n}| \leq \frac{1}{n}$ (and this holds whether or not $\alpha$ is irrational).
The converse of Dirichlet’s theorem is true as well: if $\alpha$ is rational then there are only finitely many reduced fractions $m/n$ with $|\alpha - \frac{m}{n}| \leq \frac{1}{n^2}.$ So Dirichlet’s theorem allows us to distinguish rational numbers from irrational ones in a rather interesting and non-trivial way.
The exponent of 2 in Dirichlet’s theorem cannot be improved, since by a famous theorem of Klaus Roth (for which he won the Fields Medal), if $\alpha$ is an algebraic number then for each $\epsilon > 0$ and every constant $C>0$ , there are only finitely many reduced fractions $m/n$ with $|\alpha - \frac{m}{n}| \leq \frac{1}{C n^{2 + \epsilon}}.$
The constant term in Dirichlet’s theorem can, however, be improved. This is the subject of Hurwitz’s theorem, to which we turn in the next section.
Dirichlet’s Approximation Theorem has a number of applications, e.g. it can be used to prove that Pell’s equation $x^2 - dy^2 = 1$ has infinitely many integer solutions for every non-square positive integer $d$ . And the Stern-Brocot tree (or, equivalently, the theory of continued fractions) can be used to explicitly find all solutions.

Hurwitz’s theorem

As a motivation for Hurwitz’s theorem, we note that if $\alpha = 1/\phi$ is the inverse-golden ratio, a simple calculation shows that for any $C>\sqrt{5}$ there are only finitely many reduced fractions $m/n$ with $|\alpha - \frac{m}{n}| \leq \frac{1}{C n^2}.$

Indeed, let $\alpha' = (-1 -\sqrt{5})/2$ denote the other root of the quadratic polynomial $f(x) = x^2 + x + 1$ satisfied by $\alpha$ . Then since $f(x)$ has no rational roots, for any rational number $m/n$ we have $f(m/n) \geq 1/n^2$ . Writing $f(x) = (x-\alpha)(x-\alpha')$ , we see that if $|\alpha - \frac{m}{n}| \leq \frac{1}{C n^2}$ then $\frac{1}{n^2} \leq |\alpha - \alpha| \cdot |\alpha - \alpha'| \leq \frac{1}{C n^2} |(\alpha' - \alpha) + (\alpha - m/n)|.$ After a bit of algebra, we see that this implies $C(C-\sqrt{5})n^2 < 1$ , which (since $C>\sqrt{5}$ ) cannot hold when $n$ is large.

Adolf Hurwitz proved that $1/\phi$ , and the corresponding constant of $\sqrt{5}$ , is the “worst-case scenario” in Dirichlet’s theorem:

Adolf Hurwitz

Theorem (Hurwitz): If $\alpha$ is a positive irrational number, there are infinitely many reduced fractions $m/n$ with $|\alpha - \frac{m}{n}| \leq \frac{1}{\sqrt{5} n^2}.$

Proof of Hurwitz’s theorem

As a warm-up, we use the Stern-Brocot tree to give a quick proof of Dirichlet’s theorem. Indeed, we claim that in any Stern-Brocot triple $(a,b,c)$ corresponding to $\alpha$ , either $a$ or $c$ must satisfy the conclusion of Dirichlet’s Approximation Theorem. The proof of property (g) above shows that each rational number can appear in only finitely many Stern-Brocot triples, so we’re done once we establish the claim. And the claim is easy to prove: if $a = m/n$ and $\alpha \in (a,b)$ , then $|\alpha - a| \leq |a-b| \leq \frac{1}{n^2}$ since $|a \wedge b| = 1$ and the denominator of $b = a \vee c$ is at least as large as the denominator of $a$ . Similarly, if $\alpha \in (b,c)$ then $c$ satisfies the conclusion of Dirichlet’s theorem.

To prove Hurwitz’s theorem, we refine the above observation by proving that in any Stern-Brocot triple $(a,b,c)$ corresponding to $\alpha$ , either $a$ , $b$ , or $c$ must satisfy the conclusion of Hurwitz’s Theorem. It suffices to prove this in the case $\alpha > b$ , since if $\alpha < b$ we may replace $\alpha$ by $1-\alpha$ , $a$ by $1-c$ , and $c$ by $1-a$ .

Assuming, therefore, that $\alpha \in (a,b)$ , if the conclusion of Hurwitz’s theorem fails for each of $a,b,c$ then (setting $a=m/n, c=m'/n', b=m''/n''$ ):

(1) $\alpha - \frac{m}{n} \geq \frac{1}{\sqrt{5} n^2}.$

(2) $\alpha - \frac{m''}{n''} \geq \frac{1}{\sqrt{5} (n'')^2}.$

(3) $\frac{m'}{n'} - \alpha \geq \frac{1}{\sqrt{5} (n')^2}.$

Adding (1) and (3) and simplifying using property (b) gives $\sqrt{5} n n' \geq n^2 + (n')^2.$ Similarly, adding (2) and (3) gives $\sqrt{5} n' n'' \geq (n')^2 + (n')^2.$

Adding these two inequalities gives $\sqrt{5} n' (n+n'') \geq n^2 + 2(n')^2 + (n'')^2.$ Using the fact that $n'' = n+n'$ and simplifying, this is equivalent to $2 (n - \frac{n'}{\phi})^2 \leq 0,$ where $\phi$ is the golden mean. But then $\phi = n'/n$ , which is impossible since the $\phi$ is irrational.

Beyond Hurwitz

Hurwitz in fact proved more than just the above. He also showed that one could improve on the above theorem for irrational numbers which are not ${\rm GL}(2,{\mathbf Z})$ -equivalent to $1/\phi$ (e.g. $\phi$ ). More precisely, if $\alpha,\beta$ are real numbers, we write $\alpha \sim \beta$ if there exist integers $a,b,c,d$ with $ad-bc = \pm 1$ such that $\beta = (a \alpha + b)/(c \alpha + d).$ If we replace $1/\phi$ with any real number $\alpha \sim 1/\phi$ , it is still true that for any $C>\sqrt{5}$ there are only finitely many reduced fractions $m/n$ with $|\alpha - \frac{m}{n}| \leq \frac{1}{C n^2}.$ However, Hurwitz showed that if $\alpha \not\sim 1/\phi$ , then one can do better, with an optimal constant of $\sqrt{8}$ instead of $\sqrt{5}$ . This prompts the following definition:

If $\alpha$ is a positive irrational number, its Lagrange number $L(\alpha)$ is the supremum of all $C>0$ such that there are infinitely many reduced fractions $m/n$ with $|\alpha - \frac{m}{n}| \leq \frac{1}{C n^2}.$

It’s not difficult to show that ${\rm GL}(2,{\mathbf Z})$ -equivalent irrationals have the same Lagrange number.

The Lagrange spectrum is the set of all numbers of the form $L(\alpha)$ for $\alpha$ a positive irrational number. By what we’ve already said, we know that $\sqrt{5}$ and $\sqrt{8}$ belong to the Lagrange spectrum.

Markoff and his equation

Andrei Markoff

Andrei Markoff (also spelled Markov – he’s the same mathematician for whom Markov chains are named) discovered a remarkable connection between the Lagrange spectrum and integer solutions to the Diophantine equation

$x^2 + y^2 + z^2 = 3xyz,$

now known as the Markoff equation.

In order to state Markoff’s result, we define a Markoff number to be a positive integer $b$ such that $a^2 + b^2 + c^2 = 3abc$ for some integers $a,c$ , i.e., such that $(a,b,c)$ is a solution to the Markoff equation. The sequence of Markoff numbers begins $1,2,5,13,29,34,89,169,194,\ldots$

Theorem (Markoff):

1. The Lagrange spectrum is discrete in the interval $[\sqrt{5}, 3)$ . On the other hand, 3 is a limit point of the Lagrange spectrum.

2. More precisely, the Lagrange spectrum below 3 is precisely the set of real numbers $\sqrt{9 - \frac{4}{m^2}}$ where $m$ is a Markoff number.

As one of the steps toward proving this theorem, Markoff established the remarkable fact that all integer solutions to his equation can be described by an algorithmic procedure similar to the one which we used to define the (extended) Stern-Brocot tree!

The extended Markoff tree

The observation which gets everything going is that if $(a,b,c)$ is a solution to the Markoff equation with $0 \leq a \leq c \leq b$ , then $(a, 3ab-c, b)$ and $(b, 3bc - a, c)$ are also solutions (in the same numerical order). We’ll call $(1,1,1)$ and $(1,2,1)$ the degenerate Markoff triples, and all other solutions $(a,b,c)$ with $0 < a \leq c \leq b$ non-degenerate Markoff triples. The smallest non-degenerate Markoff triple is $(1,5,2)$ .

The extended Markoff tree $\tilde{M}$ is a rooted tree in which each node is labeled with a Markoff triple, with the root node labeled $(1,1,1)$ . The unique child of $(1,1,1)$ is $(1,2,1)$ , and the unique child of $(1,2,1)$ is $(1,5,2)$ . The subtree consisting of the node labeled with the non-degenerate Markoff triple $(1,5,2)$ and all its descendants is an ordered binary tree: if a node is labeled by the non-degenerate Markoff triple $(a,b,c)$ , its left child is labeled $(a, 3ab-c,b)$ and its right child is labeled $(b,3bc-a,c)$ :

The extended Markoff tree, from [2]

The following result is surprising, but not very difficult to prove:

Theorem (Markoff): Every integer solution $(a,b,c)$ to the Markoff equation with $0 < a \leq c \leq b$ appears precisely once in the extended Markoff tree.

The Markoff tree and the uniqueness conjecture

We obtain the Markoff tree M from the extended Markoff tree $\tilde{M}$ in the same way that we obtained the Stern-Brocot tree from its extended version: by forgetting $a$ and $c$ and just keeping the middle element $b$ of each Markoff triple. The Markoff numbers are (by the symmetry of the Markoff equation) precisely those numbers which appear somewhere in the Markoff tree.

The major unsolved problem in the subject is:

Conjecture (Markoff’s Uniqueness Conjecture, Version 1): Every Markoff number appears exactly once in the Markoff tree.

The interest in this conjecture stems partly from its apparent degree of difficulty and partly from its interesting implications. For example, the uniqueness conjecture is equivalent to the following statement which does not mention Markoff’s equation at all but relates directly to the Lagrange spectrum:

Conjecture (Markoff’s Uniqueness Conjecture, Version 2): If $\alpha,\beta$ are irrational numbers with $L(\alpha)=L(\beta) < 3$ , then $\alpha \sim \beta$ .

For an extensive history and mathematical discussion of the Markoff uniqueness conjecture (in these and other forms), see the lovely book [2].

Concluding remarks:

The basic properties of the Stern-Brocot tree yield a constructive proof (which does not make explicit use of the extended Euclidean algorithm) that if $m,n$ are relatively prime positive integers then there are positive integers $x,y$ such that $my-nx=1$ . (Take $(a,b,c)$ to be the triple corresponding to the rational number $m/n$ and let $x/y = c$ .)
Achille Brocot was a French clockmaker who used the Stern–Brocot tree to design systems of gears with a gear ratio close to a particular desired value.
Another characterization of equivalence is that $\alpha,\beta$ are ${\rm GL}(2,{\mathbf Z})$ -equivalent if and only if their continued fraction expansions coincide from some point onward (i.e., they have the same “tail”); see [2] for additional information.
There is a real number $F$ , called Freiman’s constant, such that every real number greater than $F$ belongs to the Lagrange spectrum but for every $\epsilon > 0$ there is a real number in $(F-\epsilon,F)$ which does not belong to the Lagrange spectrum. Explicitly (as you would no doubt guess), $F = \frac{2221564096+283748\sqrt{462}}{491993569} \approx 4.5278\ldots$ In the interval $[3,F]$ the Lagrange spectrum is complicated (a fractal-like blend of discrete and continuous parts).
The Stern-Brocot tree is closely related to Farey sequences, which are in turn closely related to Ford circles. Ford circles allow for an appealing geometric visualization of the Stern-Brocot tree: