I am very sad to report that my Ph.D. advisor, Robert Coleman, died last night in his sleep at the age of 59. His loving wife Tessa called me this afternoon with the heartbreaking news. Robert was a startlingly original and creative mathematician who has had a profound influence on modern number theory and arithmetic geometry. He was an inspiration to me and many others and will be dearly missed.
Robert was born on November 22, 1954 and earned a mathematics degree from Harvard University. He subsequently completed Part III of the mathematical tripos at Cambridge, where he worked with John Coates and made important contributions to local class field theory. By the time he entered graduate school at Princeton, Robert had essentially already written his doctoral dissertation, but his formal thesis advisor was Kenkichi Iwasawa. He began teaching at UC Berkeley in 1983 and was a recipient of a MacArthur “Genius” Fellowship in 1987. Robert published 63 papers, including 8 papers in the prestigious journal Inventiones Mathematicae and 5 in the Duke Mathematical Journal. He had an amazing intuition for everything p-adic. Long before the invention of Berkovich spaces, Robert could somehow visualize paths and structures in p-adic geometry which no one else in the world saw as keenly or as profoundly. I rarely saw him reading papers or books. He seemed to figure out whatever he needed to know almost from scratch, which often made his papers quite difficult to read but this went hand in hand with his brilliance and originality.
When I was a graduate student at Berkeley, Robert hosted an invitation-only wine and cheese gathering in his office every Friday afternoon code-named “Potatoes”. Among the regular attendees were Loïc Merel and Kevin Buzzard, who were postdocs at the time. It was a wonderful tradition. In the summer of 1997, while I was still a graduate student, Robert invited me to accompany him for three weeks in Paris to a workshop on p-adic Cohomology at the Institut Henri Poincare. That was the first time I met luminaries like Faltings, Fontaine, and Mazur. Since the workshop was (a) totally in French and (b) on a topic I knew almost nothing about, I was in completely over my head. But I fell in love with Paris (which I’ve since returned to many times) and my best memories from that trip are of dining with Robert and seeing the city with him.
The trip also taught me to appreciate the significant challenges which Robert, who had Multiple Sclerosis, bravely faced every day. I remember helping Robert check into his hotel room near the Luxembourg Gardens, only to find out that his wheelchair did not fit in the elevator. We had to find another hotel room for him, which was not so easy given the level of our French! Curbs were a constant challenge for Robert, as finding on- and off- ramps for wheelchairs in Paris was like trying to get a vegan meal in rural Arkansas.
Robert hosted a Hoppin’ John party at his house every year, and it was delicious. (It’s somewhat ironic that I now live in the South but the only place I’ve ever had Hoppin’ John was in Berkeley, California.) Robert had a mischievous and impish sense of humor, and consequently he surrounded himself with colorful and funny people. For many years Robert’s closest companion was his guide dog Bishop, who would join Robert everywhere. Bishop eventually passed away and Robert found a new canine companion named Julep.

In the wedding party with Robert and Tessa
My advisor was always very supportive of me, and I owe him a tremendous debt of gratitude for helping me obtain a Benjamin Peirce Assistant Professorship at Harvard after I graduated from Berkeley. That position helped my career in immeasurable ways. More recently, Robert helped recruit me for a professorship at Berkeley where I spent a memorable year as his colleague during the 2011-12 academic year. (I eventually returned to Georgia Tech for family reasons.) It was wonderful to reconnect with him, introduce him to my kids, and meet his lovely fiancee Tessa, who he married in Summer 2012. I was very touched and honored that Robert asked me to be in his wedding party, and I’ve never seen him as happy as he looked on his wedding day. I am heartbroken for Tessa, who has been so fiercely devoted to Robert.
Robert Coleman’s fundamental contributions to mathematics include:
- His Ph.D. thesis “Division Values in Local Fields”, worked out when Robert was still an undergraduate and published in Inventiones.
- His theory of p-adic integration, introduced in his seminal 1985 Annals of Math paper “Torsion Points on Curves and p-adic Abelian Integrals”. Coleman’s theory has had significant applications to the theory of rational points on curves, starting with his Duke paper “Effective Chabauty” and continuing to the present day with non-abelian analogues due to Minhyong Kim and others. The method of Coleman-Chabauty is currently one of the best ways to explicitly calculate the rational points on a curve of genus at least 2. Coleman’s method of proof, which he calls “analytic continuation along Frobenius”, helped inspire Kiran Kedlaya’s influential p-adic algorithm for counting points on hyperelliptic curves over finite fields, which is important in modern cryptography. Coleman’s theory of p-adic integration has been generalized by Colmez, Berkovich, and other prominent mathematicians.
- His work on p-adic families of modular forms, introduced in his 1996 and 1997 Inventiones papers “Classical and Overconvergent Modular Forms” and “p-adic Banach Spaces and Families of Modular Forms”. These papers introduced important new methods from the theory of Banach spaces, coined the term “overconvergent modular form”, and proved an important criterion for such a form to be classical. Those papers, along with Coleman’s subsequent work with Barry Mazur constructing the so-called “eigencurve”, have had a huge impact on the theory of Galois representations.
- A new proof of the Manin-Mumford conjecture, influential work on stable models of modular curves (which Jared Weinstein has recently refined and applied to the Local Langlands Program), the Coleman-Voloch supplement to Gross’s work on companion forms, contributions to p-adic Hodge theory, and much more…
For the last year, Kiran Kedlaya, Ken Ribet, Richard Taylor, Annette Werner and I have been organizing a conference on p-adic methods in number theory in honor of Robert Coleman’s 60th birthday which is scheduled to take place in Berkeley, California in May 2015. The conference will now be a tribute to the legacy and influence of Robert’s mathematical work. It will feature an all-star line-up of speakers, including John Coates, Jean-Marc Fontaine, Barry Mazur, Peter Scholze, and many others. Stay tuned for more detailed announcements…
Robert Coleman was a kind, brave, and brilliant man whose influence on mathematics and on his friends and loved ones will long outlive his fragile body. Please share your memories of Robert as a mathematician and inspirational human being in the comments section below.
[Note added 4/8/14] There will be a memorial service on Saturday, May 31, 2014 at the Bancroft Hotel in Berkeley from 2-4pm. People are encouraged to bring remarks, pictures, videos, etc. Please let Ken Ribet (ribet@math.berkeley.edu) and Arthur Ogus (ogus@math.berkeley.edu) know if you plan to attend, and if you plan to speak or bring any mementos.

I never met Coleman, but I’ve enjoyed reading his papers. His description of analytic continuation along Frobenius is hilarious: “Rigid analysis was created to provide some coherence in an otherwise totally disconnected p-adic realm. Still, it is often left to Frobenius to quell the rebellious outer provinces.”
Matt has already described so well what a great person Robert was. He was instrumental in making the year 91-92 that I spent in Berkeley a wonderful year both personally and mathematically. He drew me into his research and taught me a lot of things. His p-adic ways and my characteristic p ways met at![\mathbb{F}_p[t]/(t^{p-1}) \sim \mathbb{Z}_p[\zeta_p]/(p)](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BF%7D_p%5Bt%5D%2F%28t%5E%7Bp-1%7D%29+%5Csim+%5Cmathbb%7BZ%7D_p%5B%5Czeta_p%5D%2F%28p%29&bg=ffffff&fg=404040&s=0&c=20201002) and we wrote that paper that Matt mentioned. I feel sorry that I haven’t kept up with him in the last few years.
and we wrote that paper that Matt mentioned. I feel sorry that I haven’t kept up with him in the last few years.
Pingback: Robert Coleman | Persiflage
Robert was an extraordinary person, in more than one way. I learnt this when I was in Berkeley in 96-97. His insightful work on desingularising the Gouvea-Mazur infinite fern into an eigencurve was work that hugely influenced my mathematical life. His papers on p-adic Banach spaces were sufficiently far from my comfort zone that it was hard work for me to read them, but I discovered an effective approach — I worked hard enough to crystallise any questions I had and then went to Robert’s office and asked him them; he would always answer instantly and thus keep me moving in the right direction. He was sometimes too physically weak to say more than a couple of sentences, but he was so mentally alert that they were always the right ones. During this time I got to know him as a person as well as as a mathematician, and it was then when I realised how much work real life was for him. How did he find time to do mathematics, given that it seemed to take so much time to do anything else, things I take for granted? But clearly he could find time somehow.
In London, where I live now, during the term times we usually have two study groups and the number theory seminar all on a Wednesday afternoon. Two or three years ago I remember noting one afternoon that even though the topics were rather covering a lot of modern algebraic number theory (a study group on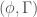 -modules and their applications, a study group on
-modules and their applications, a study group on 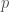 -adic modular forms, and the seminar was on computational methods for rational points on algebraic varieties) Robert’s work had been a critical component of all three lectures I heard that day — the first was on the Coleman homomorphism, the second on Coleman families and the third used Coleman’s explicit Chabauty. A wonderful and genuinely coincidental moment of synchronicity which only underlined how much Robert has influenced modern number theory.
-adic modular forms, and the seminar was on computational methods for rational points on algebraic varieties) Robert’s work had been a critical component of all three lectures I heard that day — the first was on the Coleman homomorphism, the second on Coleman families and the third used Coleman’s explicit Chabauty. A wonderful and genuinely coincidental moment of synchronicity which only underlined how much Robert has influenced modern number theory.
There is so much to say. For the last seven years, professor Coleman has inspired and influenced me both mathematically and personally.
Our association began during my junior year of undergrad, which was my first year at Cal. And the first class that I had, on my first day, was honors linear algebra with Professor Coleman. That class had the heaviest workload of any class I ever took! The long and challenging problem sets served as a catalyst for some of the best friendships I made during my college years. I remember one problem in particular that drove my classmates and I nearly crazy, and our best attempts yielded nothing – and after days we resorted to trying to guess-and-check 4 x 4 matrices. Eventually we found a way without guessing and solved the problem. The answer was quite a horrible looking expression, and in no way guessable . In class, Coleman asked to see our solution. I’ll never forget the look on his face when he saw it – he basically recoiled in surprise. I guess that there was a mistake in the problem which made it inordinately more difficult.
Soon Coleman and I became close. Unlike most professors, I didn’t find him intimidating at all. This isn’t because he was in any way less successful or brilliant than the others, but rather, it was because he was so completely humble. It felt completely natural to do a senior thesis with him, and so I did.
One story that I tell often is about Julep’s (his dog’s) second birthday party. I attended, and met for the first time some of the people that were close to Robert. Several other dogs came to the party. The usual birthday stuff happened: Julep got presents and toys, as well as a nice big slice of cake. The cake was made special for the dogs from roast beef, with mashed potato icing.
I was fortunate to take many classes from Coleman – my favorites being that first linear algebra class and also a great class in local class field theory. I decided to come back for graduate school at Berkeley so as to work with him. It has been a wonderful experience, learning about the awesome world of p-adic modular forms, rigid geometry, and eigenvarieties.
I am terribly sorry for his wife Tessa, and my condolences are with her. Still, it brings me unimaginable joy to know that the last years of his life were spent in that relationship, which I know made him very happy. This is something that I firmly believe Coleman deserved. You see, for all the amusing anecdotes (which reflect his unyielding sense of humor) and mathematical ideas, perhaps the most memorable thing about him is how optimistic and positive he was. And this despite his illness – it is truly, truly amazing. Whatever struggle I felt I had in life, or perhaps when I felt down or blue for whatever reason, it was never once that I still felt that way when leaving our weekly meetings. His positive energy was completely contagious, and the difficulties that he overcame put my own concerns into perspective. The net result of that was the greatest contribution that Robert Coleman made to my life.
I attended “Potatoes” when I was visiting MSRI in 1998. Potatoes themselves were never featured in any way. Does anyone know where the name came from?
Long ago, there was a restaurant in Harvard Square called something like “One potato, two potato.” Friday afternoons, people from the math department — I think led by Robert, Brad Osgood, and Greg Anderson — used to gather there for a drink. When Robert moved, he brought the name with him and kept the tradition alive.
Ah, I remember that place! I never went inside, but I walked by it often during graduate school. It closed down in the summer before my final year.
Thanks, everyone, for the lovely comments. Frank Calegari has also written a nice tribute: http://galoisrepresentations.wordpress.com/2014/03/25/robert-coleman/
I remember well a dinner at Robert’s house with Kevin and Bas Edixhoven (at which we ate slightly sandy razor clams). I remember as well another visit to Berkeley when I stayed with Robert, and in the morning Bishop would come bounding into my room.
I’m very glad I had those and other chances to know Robert personally, as well as the chance to engage with his wonderful mathematics. The person and the mathematics were both so inspiring.
Like many others, I’ll miss him.
Here’s a comment I received from Dick Gross which he gave me permission to post:
I remember spending a MacArthur meeting with Robert at the Hotel Nikko in Chicago. There were lots of panels and activities arranged for the Fellows, but all we did was sit around the lobby and discuss companion forms. He explained wide-open spaces, how to glue them along annuli, how this gave a great picture of the p-adic points of , etc. This was the beautiful world that Robert lived in — I felt honored to be able to visit him there.
, etc. This was the beautiful world that Robert lived in — I felt honored to be able to visit him there.
Someone asked for the origins of the Potato Society. In Fall of 1978 or 1979 I purchased a case of Australian wine (Jacob’s Creek Cabernet?) from the Wine and Cheese Cask and had it delivered to my cubicle in the math department at Harvard, meaning to take it home. Instead, a group of us started drinking it when the cheap Egri Bikaver the department served for Friday afternoon wine and cheese ran out. When the case was finished we started going down to the Wine and Cheese Cask for supplied an having our own wine and cheese in my cubicle area. Greg Anderson, Robert Coleman, Robert Indik and Brad Osgood were regulars. In Fall of 1981 we moved into to Brad’s office, and started going out to One Potato Two Potato for dinner afterwards. When Robert moved to Berkeley he continued the tradition there (it died out at Harvard after we all left). Robert and I started working together while he was at Harvard and he was responsible for me being hired as a post-doc at Berkeley in 1984, where we continued to collaborate. I last saw Robert when I flew out from Tucson to attend his 50th birthday party in 2004. I’m glad I did that. He was one of the best mathematical minds I ever interacted with. I always found his papers lucid and clear (not a widely shared opinion, I understand).
I will be representing the Potato Society at his memorial service on Wednesday.
Thanks, Bill and Jeremy — it’s great to finally learn the secret origins of the Potato Society!
Here’s another story about when Robert first came down with MS. He was on a visit to Japan (some time in 84-85?) and had a couple of strange incidents: being unable to hit the ball in tennis, stumbling on the stairs in the subway. The Japanese doctors didn’t know what was going on. When he got back to Berkeley he was diagnosed with MS. From that point he had a shockingly rapid descent that caught his doctors by surprise; for many patients MS is a long slow decline. He went from perfectly healthy to the verge of death within a matter of weeks. His decline was arrested by some experimental and aggressive chemotherapy treatment. After that he recovered slightly, to the point where he could come home and get around with the aid a wheel chair. But he never bounced back the way MS patients sometimes do. For the first few 6 months or so I was his chauffeur to and from work (his wife Eliza didn’t drive). I would pick him up at his house on Seaview Drive in my Toyota Tercel every morning, folding up the wheelchair into the hatchback. In those days he could get himself down the stairs with someone holding him by the elbow; later he had a ramp installed around from the back.
He and his first wife Eliza were on the verge of separating when he came down with the disease, but she stayed on to help him through the rehab. We also got to meet Robert’s sister Rosalind at that time, when she came out to help. Later, when our first daughter was born in 1986, Robert and Eliza cooked us months and months worth of frozen meals, in gratitude for the help we had provided. She was colicky for the first 6 months and I don’t think we (or she) would have survived without them. I’ll have to tell her she owes her life to Robert.
For those of you who are in the area or want to send flowers, I’ve just been informed by Ken Ribet that the funeral service will take place tomorrow (Wednesday March 26) at 3pm:
Sunset View Mortuary
101 Colusa Avenue (at Fairmount)
El Cerrito CA 94530
Robert deserves more than I can write here off the cuff, but I do want to add “Division Values in Local Fields” to Matt’s list of Robert’s accomplishments. I am pretty sure he did this work when he was an undergraduate visiting Coates in Cambridge. It’s one of the foundations of the modern applications of p-adic analysis to arithmetic.
Thanks, Jeremy — I had mentioned this in the introduction but I’ve now added it to the list of Robert’s accomplishments at the end as well.
I think it was when Robert was giving a talk on ‘Division Values in Local Fields’ at Harvard that I was introduced to him by Jonathan Lubin, perhaps 1979? Almost a decade later, I saw his elegant paper “One-Dimensional Algebraic Formal Groups”, (“Every algebraic formal group is algebraically isomorphic to a formal algebraic group”), and wrote to him suggesting the methods would apply to a puzzle I heard from a seminar of MacPherson at Brown. He wrote back very quickly (those were still the days of hand-written notes…), and after I suggested a small tweak, very generously gave me co-author ship on the resulting note: “Rational Formal Group Laws” (Pac J (147)). I’m so proud of being his coauthor, and am very sad to hear of his premature death, and wish I had known him better.
I think that I first met Robert at a workshop in early 1989, in
Tucson, Arizona. It was probably partly due to him that I got a two
year position in Berkeley after my PhD defense that same year.
Those two years in Berkeley were wonderful, and Robert was one of the
most important people for me there, both mathematically and
socially. He took real interest in my work. I learned a lot from a few
graduate courses that he taught, and of course from the discussions
that we had. In the weekends we often made trips with John and Marisa
Castellano, visiting parks in the Bay Area, we on mountain bikes and
Robert with his Cobra wheelchair. He invited me regularly to dinner
parties at his house, with wonderful food (I’m to blame for the
sandiness of the razor clams mentioned by Matthew Emerton) and with
wonderful people with many different backgrounds.
I first met Robert Coleman in 1990, when he was having a barbecue at
his house, and I accompanied Bas Edixhoven, whom I was then
visiting. Though he didn’t know me, Robert was very friendly, making
me feel right at home. I saw him again when he visited Bas in Rennes
in the spring of 1995, with one of his students. I remember a trip to
the swimming pool and visiting the Northern coast of Bretagne for a
weekend. The third time I saw him was in 1997, when Bas, our son Luc,
and I spent about three months in Berkeley. Robert had just gotten
Bishop. Robert was a great person to be around and I will remember him
fondly.
I had the good fortune to meet Prof. Coleman at a critical juncture in my life.
I was feeling pretty down because all of my summer plans for mathematics had fallen through. I felt lost and I guess I was looking especially sad, because Prof. Coleman asked me what was wrong. This was the first time a professor had ever asked me a personal question! I was a bit shocked, afraid I had misinterpreted him, but he persisted. When I related my situation, he was sympathetic, and offered to meet with me if I wanted somebody to talk mathematics with.
Reading with Coleman was fantastic, but only much later did I realize how exceptional this experience was. First of all, he was supremely patient and generous with his time; sometimes our meetings would begin after lunch and end only when he received a call that his ride had arrived, at which point Julep would start digging fervently in the corner and drown out all chance for further conversation. Second, he had a powerful and deep intuition for anything p-adic. Whether it was technical details with tricky sums and integrals or a vague big picture question about what’s “really going on” he was equally lucid. As he introduced me to his circle of ideas and the beautiful world of p-adic modular forms and rigid geometry, I was struck with how clear these objects were to him, and he always had these lively explanations and conjectures about some of the aberrant behavior that I could not find anywhere else. Years later, I realized that not everybody could see these things in the same way he did. Finally, he was always energetic and positive and very funny. When an idea didn’t work out, he just shrugged, smiled, and would start up a new line of attack, unfazed. “I got a million of ‘em!” he’d say. He encouraged me to pursue graduate study and gave me questions to think about, all while telling me to develop my own personal view of mathematics, and I would always leave our meetings with a hopeful feeling.
I remember asking him one time why he decided to study p-adic analysis, and he said “Because it’s easy!” with a gleam in his eye. I first took this literally, but upon reflection, it was with this that he taught me an important life lesson:
“Because it’s easy!” because mathematics should be fun and a source of joy and inspiration in your life.
“Because it’s easy!” because I can tell you’re scared, and this will give you the confidence to continue fighting the good fight.
“Because it’s easy!” because, actually, it is quite difficult, but we need all the help we can get.
I am glad to have had the privilege of having Prof. Coleman as a teacher, a mentor, and a friend. I will miss him deeply.
I met Robert at the Institut Poincare workshop in Paris during the summer of 1997. Several nights we went out to explore recommended restaurants, mostly in some obscure alley and quite hard to find. It was always an adventure to navigate Paris sidewalks in Robert’s chair, but this never stopped him. Robert was so open and interested in everything. He was an outstanding and inspiring mathematician with a fantastic intuition, which I found sometimes quite hard to follow. He was also a wonderful person and it was so much fun to discuss the rest of the world with him. I will miss him.
From Barry Mazur:
How many places in the world get their intensity, in my memory, because they were where Robert Coleman and I worked together; places where I experienced his thoughts, and his ways of thought. From lunches at the Musical Offering in Berkeley where I learned about his ‘Coleman Families,’ to the jaunt along Hadrian’s Wall we made in our rented Rover together starting out at St. Cuthbert’s tomb in Durham Cathedral. We drove to point after point of that long barrier built to separate the Romans from the barbarians. Through un-mowed summer grass hiding ruts and grooves Robert would maneuver his wheelchair to descend to the wall. And all the while he continued the conversation about whether the eigencurve might have finite or infinite components.
Three weeks before he died, Robert told me of his extraordinary idea about the rim—the rim of that same eigencurve. Robert focused on what is important in mathematics and in life—from beginning to end, and that’s a trait to try to emulate! He had the imagination and originality (and the courage) to work on only crucial ideas, those that just verge on the possible; those that his energy and vision made possible. He was unafraid to dream the great dreams of his subject.
I first met Robert in the fall of 1975, when he was the grader for a course I was taking. The following series of emails from him from 1990 captures something ineffable:
Good time to get a cat or maybe
a dog which I can train to tow my mountain wheelchair. I’ve been
heading into the wilderness Point Reyes, Mount Tam, Big Basin etc.
with a chair designed to go off road. I can push it myself but to get
anywherew in a reasonable amounyt of time I go with nmountain bikers
who tow me while I push.
I have a Cobra which is an offroad manual wheelchair. I met
the ewngineer laast fall. I have the third one he’s made. He and his
wife and I have gone on trips to Point P{inole Big Big Basain and up
Mount Tam. They put tow ropes on the chair when we went up Mount Tam
and through Big Basin. It was John who suggested the dog idea. John
is the engineer.
Perhaps Robin gottlieb mi9ght be a good cat saittewr in
Boston. Don’t worry, I am learning to type properly i.e. w/o looiking
at my fingeras. That is why thetre are so many typos.
I don’t know what I will do in Europe besides Paris and
banlieu and Padua.
I am taking care of a potential cat. It isw not working out.
I practically never see him. He prefers the basement to my company.
This cat does not like me. I’ve tried canned food, tuna fish
and icecream. I’ve spoken to it nicely. I’ve let it roam where it
wants. It wants to stay in my basement and only to come up to eat and
use the litter box.
Berkeley is the same as always. Some new restaurants, some
old restaurants gone. Some new visitors, some old. I’ve had two
BBQ’s, I am learning TeX and to type. I am worrying about monodromy
and getting in over myhead.
The cat has disappeared.
You did not send me any preprints.
I am now trying to understand monodromy. All the hot shots
tell me to read Grothendieck and Deligne but I have not gotten to the
point where I can see the clarity of their approach. I just found a
paper by A’Campo which explicitly describes what’s going on.
I was woken up fro a nap yesterday by someone munching on some
kibbles. I went into my kitchen, the outside door to which I left
open and lo just outside the door stood thed kitten. I called John
and told him the cat had come back (I was taking care of the cat for
John and Marisa while they were away and could keep him if we got
along.) I told him it was unlikely I could catch the cat since I
doubted he wqould let me get between him and the door. But I was
wrong, with a little ice cream in a dish I caught the cat off his
guard and closed the door while he was in the kitchen. John cvame
ove4r and took the cat away. It was sad to see him go but he is just
not used to people (he was a stray) and we just weren’;t made mfor
eash other.
That is fabulous, Alice.
From Ehud de Shalit (posted with his permission):
Dear Matt,
This is very sad news. I have read the beautiful eulogy you posted – I believe we all share the same feelings.
I was fortunate to see him last month, on my visit to MSRI. He was in great spirits and it seemed that Tessa really made his last years very happy. The two of us even drove to a concert in Oakland together (Tessa had some swimming session that night) and as much as getting in and out of the van or just communicating were uneasy tasks, he was enjoying every moment of it. Nothing indicated that his death was so near.
I have learned a great deal from him – about math and about life.
Best regards,
Udi
My thesis was about torsion points on curves (specifically, making the Manin-Mumford conjecture explicit for certain modular curves). Robert once said to me “I think I finally understand why the Manin-Mumford conjecture is true — torsion points are just too fat.” He never elaborated on this. To me, that remark is a classic example of Robert’s mysterious (and occasionally frustrating) but always provocative way of discussing mathematics. I would conjecture that he had anticipated something along the lines of the Szpiro-Ullmo-Zhang theorem, since implicit in the proof of that result is a “repulsion principle” for points of small height. However — as with a great magic trick — some mysteries are perhaps best left unanswered.
I met Robert as an undergraduate at Berkeley. I never took a course from him, but it turned out I could use a result he and Bill had at the time recently proven to prove a conjecture I had somehow come up with on power residues. That’s when I started to get to know him a bit: I can’t recall the name of his wonderful dog, but it worked really hard to get him around all kinds of places in the 90’s. I spent a lot of time staring at his papers in those years (and to continue the tradition, had one of my students stare at his papers more recently). One time in the earlier 2000’s, I was in town to give a talk around the holidays. I think Robert didn’t realize I was actually from the Bay Area and staying with my parents, so, as I saw it, he took pity on me by inviting me over for a party he was having. I’ve recalled that kindness ever since. I last saw him in 2012 in Seoul, where I got to meet his wife Tessa. He was clearly as sharp as ever, though less able to communicate. I wish we could have talked more.
I met Robert at Harvard when I arrived in 1981, and I got to know him a little bit better when I took his course on Modular Forms. That course was the foundation of everything I ever knew about the subject; he was clear, he was thorough, and he was fun. I took voluminous notes, which are somewhere around my house or office. His course made it possible for me to come to grips with all of the exciting mathematics that was happening around me at that time. Later, in conversations, he was a constant source of encouragement and ideas.
I’m pretty sure that my last visit to see Robert in Berkeley took place the week of September 9, 2001. I was visiting MSRI, and I woke up the morning of Tuesday, September 11, 2001 at his place, just as Bob Edwards was announcing the fall of the first tower. With the shutdown of air travel, I ended up spending that very stressful week with him.
Of course Robert was brilliant, but what really impressed me about him was how relentless he was when it came to mathematics. He simply never gave up in the pursuit of an idea. I spent a few visits staying with him at his house, and it was absolutely exhausting. Whatever idea we were talking about, Robert returned to it, over and over, from all different points of view, trying to get traction. From him I came to understand that it’s not enough to be really, really smart to be a great mathematician, you have to be consumed by the subject and you have to have the stamina to work and work and work. I knew I would never be as smart as Robert — and I came to realize I could never work as hard as him, either.
When his MS had made his hands shake and his voice slur, he brought that same determination to bear. I watched him spend hours typing slides for his lectures so that he could keep teaching — things that should have taken an hour would take half a day, but he did not give up.
I am particularly grateful for one particular contribution. When Schneider and I were thinking about the ideas in the paper “p-adic Fourier theory,” Robert made a visit to Chicago. I had lunch with him at some godawful hotel in the western suburbs — he was visiting his brother, I think — and I told him about the problem. I remember him saying that there ought to be a formal group in there somewhere, and that turned out to be the crucial idea we needed to get that paper going. I think that paper is my favorite among my own work, and Robert was key to finding the theorems.
Through his mathematical work, Robert’s name will certainly live on. More importantly, though, his personality — his courage, his sense of humor, his kindness, and his generous spirit — will live on in my memory and in the memory of so many people who knew him in the mathematical community and beyond.
I took honors analysis with Professor Coleman my sophomore year at Berkeley. The class was unusually small, with only me and one other student, along with the TA. I remember that it was quite difficult to follow the lectures (due to the Professor’s difficulty with speaking at length), but we never had problems since he took the time to type out careful notes for the class.
I vividly recall our final. He gave us a sheet with 50 problems a week before the exam and told us that 10 of them would be on the test. I spent the next week working non-stop to figure out the problems. I’d never had so much fun in a math class, and looking back, I think it was really that one course which convinced me to become a math major.
I’m very sad to hear that he’s passed away. My condolences to his wife and friends.
I learned this sad new from Mrs Coleman yesterday. I was shocked since about four weeks ago I sent an email to him consulting him the transcendence of an Eisenstein series and he offered me with ideas and references which helped me work out the problem. I never expected it would the last email I received from him.
I met Prof Coleman in January last year when I was visiting Berkeley as an exchange student. I was fortunate to attend his course on elliptic curves and modular forms. After that semester, I stayed at Berkeley working on a research project supervised by him. It was about Elkies’s construction of an infinite family of elliptic curves with large Mordell-Weil rank.
Prof Coleman was a very kind and responsible to his students I remeber once I was sick he sent emails to me asking my health condition and if he needed to change the weekly meeting. Even after I coming back to singpaore, he cared about my progress in mathematics and offered me invaluable guidance.
I learned a lot from Prof Coleman, both in mathematics and his brave and optimistic altitude towards life. I will deeply miss him.
It is really sad news, and I share the feelings Matt expressed in his eulogy. Matt has described well Robert’s important contributions to mathematics. If I may, I would like to tell about my experience in studying just one of them, which convinced me that Robert, as Arthur Ogus wrote, is a fabulous mathematician.
When I was visiting MPI Bonn in summer 1996, I studied Robert’s work on p-adic integration several of my colleagues told me about. I am referring to two of his Inventiones papers: the 1982 “Dilogarithms, regulators and p-adic L-functions”, and the 1988 “p-Adic regulators on curves and special values of p-adic L-functions”, which Robert co-authored with Udi de Shalit. The new p-adic phenomenon he discovered in those papers was even more striking than the brilliant applications of it he has found. This phenomenon is an analog of the following property of a smooth complex analytic space: if the space is simply connected, any closed analytic one-form has an analytic primitive. Of course, the same cannot be true for smooth p-adic analytic spaces. But Robert showed that each so called basic smooth p-adic analytic curve is provided with a bigger class of locally analytic functions such that any one-form with coefficients in that class has a primitive in the same class and is defined up to a constant. Furthermore, functions from that class behave like analytic ones, e.g., they satisfy the uniqueness property. Robert’s discovery fascinated me as much as that of p-adic uniformization of Tate elliptic curves I learned when I was an undergraduate student. This time, however, I was already working on this subject for several years, and eventually was able to show that the same phenomenon takes place for smooth p-adic analytic spaces of arbitrary dimension. This was done using main ideas of Robert’s work and new technical tools which became available later. Needless to say that the full explanation of this phenomenon is yet to be found.
I was fortunate to meet Robert on a number of occasions. The first time was in Trento in 1989 and the last time was in 2009 in Berkeley. Robert was an exemplary mathematician who will be missed by all who knew him.
From Jean-Marc Fontaine:
This is indeed a very very sad news. We all know how deep are the mathematics of Bob. We also all remember his infinite kindness and his unlimited generosity. Long time ago, I invited Bob to visit us in Grenoble and he spent about three months there. We enjoyed doing mathematics but also walking in the mountains around. I still remember very well a day where I invited him to come to the small house I rented with my family in the « massif de la Grande Chartreuse ». He saw two kids living next door to his place who looked unhappy, so he did a thing that only he could do : he asked them to come with him in the small french car (a « 4L ») he had bought. These two kids and all of us, we had a wonderful day.
If I remember correctly, he was caught by multiple sclerosis almost immediately after he came back to Berkeley. It didn’t stop his unlimited generosity. But we also learned that his courage was also unlimited. I won’t forget his stay in Paris during the p-adic semester in 1997. At this time, Paris was not equipped at all for people in wheel chairs (it is still not so good), but he never complained, managed to participate to all activities and everybody loved him.
Please express my deep sympathy to his family and his relatives.
I met Robert for the first time in Arcata when he was still healthy (I remember we played ping-pong together), but it was in 1986, immediately after he was struck with MS, when we became close friends. His way of thinking about the p-adic world influenced much, if not all, of my early work. Besides our joint paper on p-adic regulators on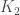 of curves, there was work on the explicit reciprocity law, on p-adic periods of
of curves, there was work on the explicit reciprocity law, on p-adic periods of 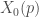 , on p-adic Eichler Shimura cohomology, and on a formula for the cup product on Mumford curves – in all of which Coleman’s point of view played a dominating role, which I probably neglected to acknowledge at the time.
, on p-adic Eichler Shimura cohomology, and on a formula for the cup product on Mumford curves – in all of which Coleman’s point of view played a dominating role, which I probably neglected to acknowledge at the time.
It was mentioned that Robert’s official Ph.D. advisor was Iwasawa. Not less influential in those early Princeton days was Dwork, whom Robert admired, and whose “function analytic” way of thinking about the p-adic world he adopted.
We had a BSF grant together, and Robert visited me twice in Israel. He did not let his illness hold him back and we toured Israel from Jaffa to Jericho, and from the Dead Sea to the Galilee, even when, on one occasion, Pan Am left his wheel-chair behind in NY… (it was later delivered). When Navah and I decided to get married, Robert was the first person to get the news, simply because he had been staying with us in Jerusalem at the time.
Robert was an amazing optimist, and had a great sense of humor. He was the bravest man I have encountered. I will miss him profoundly.
I first met Robert in the summer of 1971 when we were both high school students in the Ross Program at the Ohio State University. This was my third summer in the Ross Program and Robert’s first and only, so from his point of view, I was an experienced old hand at mathematics. Bob (that’s what we called him in those days) and I spent many hours sitting around the dorms talking about mathematics. He would come to my room to show me his solutions to various problems he was thinking about. He was obviously very bright, but was not one of those flashy kids who could solve just about any problem quickly and effortlessly. Already at the age of 16, Bob preferred to wrestle with problems, to find his own ways of thinking about them, and to ask new questions of his own devising. As a result, he developed his own distinctive ways of organizing knowledge, always accurate and always interesting but rarely the “standard ways”. This puzzled me at the time, I was too young to understand the significance of Bob’s distinctive mathematical style. I had no idea that he would later provide the foundations on which much of my own research would crucially depend. Only years later would I come to recognize in our teenage interactions the early signs of Robert’s unique genius and the fresh originality of the many contributions he would make to mathematics.
Coleman was light years ahead of Steve Jobs: he was the original guy to think different. This was especially true where Newton polygons were concerned. (Steve never got into those.) I remember how obvious it was to Robert how to prove Schur’s theorem concerning the Galois groups of the polynomials obtained by truncating the Taylor series for exp(x). At first, no one could follow Robert’s reasoning. Fortunately, Robert was patient; he was always happy to provide further details.
Robert’s lectures in the 1980s were hard for people to follow because Robert hadn’t yet understood that mathematicians didn’t all see things the way that he did. I remember a seminar that he gave in Paris soon after he joined the Berkeley faculty: a very prominent French mathematician whispered to me during the lecture that the ideas seemed to be great but that the “sales pitch” was not up to standards. (“Il a de bonnes idées, mais il les vend mal”.) After Coleman’s ideas became more established, the sales pitch was no longer necessary.
We always had a great time at Potato Society. We could usually begin by opening up a couple of the bottles that were left over from the previous week. After Society members began to stream in, there were baguettes, new bottles of wine and chunks of cheese on the tables. We always managed to drag in extra people from the department who were walking near Robert’s office. Our group often included postdocs, graduate students and staff members. There’d occasionally be an undergrad, but that was exceptional. We’d always have a good view of the Golden Gate Bridge and the setting sun. Depending on the season, the sun would be north of the bridge, right at the bridge or further south. Life stopped for a couple of hours late in the day every Friday. My wine glass from that era is still on one of my office bookshelves; it shows up sometimes in photos of office hours that are posted on my Facebook page.
Our memories of Robert Coleman are a little different than others on the blog. We are not mathematicians. Robert purchased an off-road wheelchair from John back in 1989, and we used to go mountain biking with Robert and Bas back in the day when we still lived in El Cerrito. John and I would take turns towing Robert up the hills using bungee cords attached to our bikes. Sometimes we would tandem tow. And then Robert would fly downhill. Robert may have seemed meek in some ways, but he was a thrill seeker on those downhills!
My favorite memory of Robert is the time we went riding in Annadel State Park in Santa Rosa, and we were coming down Lake Trail. Near the bottom, when you’re really bombing, suddenly a sign appears: “Gate Ahead.” I’m not going to say that Robert ignored the sign, but he did have to come to a screeching halt. He said dryly, “Maybe the sign should say, “Closed Gate Ahead.”
We have many happy memories of Robert’s “potatoes” Fridays (with Bas, the Ribets, Hendrik, and others) and his Seders as well. He was not super orthodox as far as the Seders were concerned; for example, for the “bitter herbs”, we would bring a side dish of Italian broccoli rabe. Robert had a zest for life that people in much better physical condition lacked. I remember when he won the MacArthur genius award, I commented that he could pay off his house. “How boring” was his response, and he went on to do much more interesting and exciting things with that award. Rest in peace, Robert, we’ll miss you.
John adds: Robert was one of my first customers for my Off-Road Wheelchair design. We were neighbors, and started doing some rides together. He invited us for wine and cheese in his office, and that was our introduction to “Potato Society”. I was stoked to have a mathemagician friend for times of need.
One time at Potatoes, I broke the anything-but-math rule and asked Robert about a design problem I was working on. I was designing a new style of bicycle frame with a shapely “monocoque” frame. I wanted to describe the perimeter mathematically so I could generate a 3-D model for stress analysis. I wanted to fit a curve going through six points on a plane. Then I could pick the endpoints, the slope near the endpoints, and a couple of points in between to control the shape.
Robert confirmed that it was possible to find a polynomial that would go through any number of (x,y) points. I tried a parabola through three points—so far so good. For N=6, not so good. I didn’t want to bother Robert again with my lowly algebra problem, but after 16 pages of trying, I called him on the phone.
He thought about it for maybe 10 seconds and said “it’s just the summation over i and j = 1 to N of y sub i times (x minus x sub j) over (x sub i minus x sub j), for all i not equal to j”. I gulped. My (incorrect) expression took up a whole page, and his expression fit on half a line. I expanded it out for N=3—incredible. I dove into N=6 and it once again took up a whole page, but this time it was correct! I couldn’t believe he was able to state it so compactly. Now after reading everybody’s posts above, I see I was barely scratching the surface of Robert’s understanding, but receiving the full measure of his generosity. Of course, it was not the only time. I will not be alone in saying “Thanks Robert”.
Matt has mentioned my work on computing zeta functions. To put that in context, it would be best to tell a longer story.
I visited Berkeley during fall 1997 during a period in my graduate studies when I was quite unsure where to find my mathematical niche. Robert happened to be giving his course on “Fontaine’s theory of the mysterious functor” in his own idiosyncratic but brilliant style. While at the time I found it hard to digest all that was going on, the originality of Robert’s thinking was inspiring, and I think that one course had more of a direct effect on my mathematical trajectory than any other single event. For instance, my own journey to the theory of perfectoid spaces can effectively be traced back to Robert’s exposition of the field-of-norms construction for C_p from that course!
I was incredibly fortunate to have the opportunity to return to Berkeley as an NSF postdoc from 2000 to 2003. Although Robert was not even officially my sponsor, his hospitality (including Potatoes) helped create a vibrant intellectual community in which I was able to thrive. Both my work on computing zeta functions and my theory of Frobenius slope filtrations emerged from the discussion I had with Robert and his students, visitors, and collaborators.
Robert’s influence on my work even extends to some of my PhD students. Most notably, the thesis of Jennifer Balakrishnan on computing Coleman integrals sprung from an intense discussion between me and Robert at a meeting in Banff in February 2007.
Just as Dwork was the advisor Robert never had, I consider Robert to be the advisor I never had. His ingenuity, humility, generosity, wry humor (e.g., that “rebellious outer provinces” quote, which I included in my p-adic differential equations book), and courage in the face of adversity (Banff in a wheelchair? In the middle of a snowy winter?!) are models for us all. He will be missed but never forgotten.
Many people who’ve posted here have more personal stories of Coleman’s inspirational mathematics and personality. Mine is a little more indirect. I did have brief conversations with him on two occasions (once at Harvard in the early 90s, and in 2000 at MSRI); both times, he was very generous and encouraging. I’m glad I got to tell him in person that he had influenced my first steps as a mathematician through one of his papers: a little gem on algebraic properties of orthogonal polynomials (mentioned above in Ken’s post), published in 1987.
That year I was a senior in college; one day early in the fall, I gathered my courage and went to see Dwork (whom I’d never met) to ask if he would be willing to supervise my senior thesis. To my surprise, not only did he agree, but I had hardly walked in the door and stated my request before he put a bunch of photocopies in my hands saying “OK, I’ll see you every Tuesday at 1 pm.” One of the photocopies was a preprint by Coleman (typed in Microsoft Word on a Macintosh, with some comments pencilled in by the author!) to be published later that year in Enseignement Math. Master of all things p-adic (to paraphrase Matt’s description above), Coleman showed that the p-adic Newton polygon of the truncated exponential series has an elegant form mirroring the base p expansion of the degree, and went on to give a nice application to computing Galois groups. Looking back on it, I imagine that to Coleman it was just intuitively clear that the polygon had to be what it is, but he wrote a careful proof in many easy steps, and to my surprise I found I could eventually make sense of everything. What’s more, the paper ended with a series of nice “exercises,” which meant I had something I could mess around with. Strange how it’s hard to let go of problems we attempt (and fail) to solve when young…. One senior thesis and many published papers later, I keep coming back to trying to complete “exercise (b)” using methods Coleman introduced in a six-page article that occupies only a tiny corner of his mathematical output.
When I applied to graduate schools, I was admitted to Berkeley but without financial support. I was lucky to have offers from several comparable schools with generous support. Naturally, I asked Dwork’s advice on where I should go. He evaded my question, but I was a little insistent, so he finally said “OK, I don’t blame you if you don’t do this, but I think even without financial support you should go to Berkeley and study with Coleman.” I gave it serious thought, but in the end, I wasn’t [what’s the right adjective here: bold? adventurous? rich? confident?] enough to follow Dwork’s advice. When I saw Matt’s eulogy above, that conversation popped into my head as just a small illustration of the position of extraordinary respect and admiration Coleman occupies in the number theory community.
From Pierre Colmez:
It is very sad news indeed. My work was so close to Bob’s that I feel that I have lost a mathematical older brother. I met him for the first time in Grenoble, probably in 1985, and I still remember a conversation we had, back then, that had a deep and unexpected influence on my career. I will miss him.
It is heart-rending news! I remember going with him on a hike in 1979, when I first got to know him, and if anything he was the fastest walker in our small group of six, and I for one would have never imagined him getting MS later. At that time he and I were both getting interested in the dilogarithm and K_2 of algebraic curves, albeit from two very different perspectives. After that I got to learn a bit of his insightful theory of p-adic analytic continuation “along Frobenius” of the solutions of differential equations of unipotent type.
Two years ago he seemed very happy about his impending marriage, and his health seemed to be stabilizing a bit. I also have good memories of staying at his place in El Cerrito with my wife Pat for a few days in the nineties. It’s sad to think that he is no longer with us. But surely his creative work will be relevant for a very long time, and his sunny disposition will always be remembered..
I’m Robert’s sister and I want to thank all of you who posted these comments. Being only an MD — with calculus as my highest achievement in math –, I have no idea what p-adic means, but your stories and memories bring out aspects of his life that I am grateful to learn.
Thank you.
Rosalind Coleman
Bonnie Brown-Cali of dogdynamics.org posted the following nice video of Robert and Julep on YouTube: http://youtu.be/edBTLtkpVrE
Tessa, I knew the first time I met you that you were a great match for Robert. Everyone could tell — including Robert I’m quite sure — that you treated him like a person first and a person with a disability second. I know how painful it must be that you only had two years together, but I bet it felt like 20 to Robert as well and you should be very comforted by how much love and happiness you managed to squeeze into those two years. It’s great that he had someone appreciative with whom to share his exquisite sense of humor every day.
In a seminar I attended just this week, a theorem was written on the board: the classicity statement for overconvergent p-adic modular forms of small slope. The speaker, a specialist of p-adic automorphic forms, did not feel compelled to attribute the result: it went without saying. I took it as a compliment for Robert’s work, in the sense that the way it was presented showed how central and natural in the field the theorem is.
Perhaps I can share a few memories. When I was in Berkeley (1995-97), Robert was my host. As Matt reminds us, we used to meet in his office on Friday afternoon as part of the potato society. Colleagues, students, their friends and sometime families would come on an unpredictable basis. Kevin Buzzard and me were almost every time there during that period. I was happy to bring in the cheese and bread from the Cheeseboard.
I recall a tennis trophy in Robert’s office, and Robert’s specially trained dog, Bishop. Somehow, Bishop wouldn’t learn the skills expected of him and should have been considered unsuitable. But Robert kept him.
One of the last times I saw Robert Coleman in Berkeley was to see Godard’s film “Le Mépris” at the Pacific Film Archive. We had a drink after the movie. I was the one not in need of subtitles, but I am grateful to Robert for having pointed out what I had missed in the relation between the characters of the film.
Robert was my PhD advisor at Berkeley. I was one of his earlier students (3rd to graduate).
I have many very fond memories of my time in Berkeley. Everyone seemed to pass through Robert’s office for a little wine and cheese during those Friday evening Potato Society meetings. Hence my wedding present of a kiddush cup that I picked up last time I was in Israel.
Sometimes Potato Society meetings were a little more exotic. Hendrik Lenstra, returning from the Netherlands, once brought what must have been a gallon sized bucket of herring, along with a bottle of jenever. I spent much time filleting fish that night.
Robert was never one to do anything in the usual way. My weekly meeting with my advisor consisted of a swim at the gym followed by lunch at The Musical Offering. And I remember the whirlwind tour he took me on one summer – the Max Plank Institute in Germany, the IHES in France, and a p-adic analysis conference in Italy. They built a ramp for him at the Max Plank Instute that was too steep – he had to build up a head of steam to make it into the building. The ramp at the IHES was easier.
In retrospect, it was truly amazing how happily he lived his life. He never seemed upset about his MS or almost anything at all. He just carried on as if it wasn’t even relevant. Awe inspiring.
Professor Robert Coleman is a real gentleman with witty than any person I have ever seen.
I have had many memories with him in last 20 years from my school year, in special in his summer parties with other mathematicians and families.
The most unbelievable impressive one is his visit to Seoul with Tessa for the conference I organized in 2012. I remember that he was really happy on every mornings with smile and excitement for which I could not understand where such energy came from even after the long flight. Fortunately since the hotel was located next hospital, it was very safe and relieving for us to stay in long days with a chance of seeing a doctor for his conditions.
During his stay, I realized that it took extremely devoting efforts to prepare all from morning until late night with Tessa but in spite of my concerns every staff including the driver prepared very well in such warm atmosphere for Robert.
It was just months ago I stayed in his house which I never thought it could be my last meeting with him. I still vividly remember the crying voice of Tessa in the call in the morning of the accident. In regards to how Tessa devoted her time for Robert, I would like to thank again Tessa for all. He will stay in our memories ever. I deeply thank Robert for all.
Pingback: Quick Links | Not Even Wrong
Pingback: Math blog roundup | Quomodocumque
Pingback: Effective Chabauty | Matt Baker's Math Blog
There was a nice article about Robert today in the Daily Californian newspaper:
http://www.dailycal.org/2014/04/14/uc-berkeley-math-professor-robert-coleman-dies-59/
Robert’s paper on Effective Chabauty had a termendous influence on me when I was a graduate student, as I’m sure it did on many people. Although I never knew Robert well, I remain grateful to him for writing that influential paper and for the privilege of getting to know many interesting mathematicians through discussions of that work.
Robert was a kind and generous person with great wit. I am very grateful we got to know each other through my veterinary care of his beloved Golden in his home. He was very helpful to me after my dad died in 2006, and took time to explain my dad’s articles on engineering and mathematics. You will be greatly missed, Robert. With much love from Mischa
Pingback: Newton polygons and Galois groups | Matt Baker's Math Blog
My first mathematical discussion with Robert in 1994 was the defining moment of my mathemathematical career. At MSRI, while searching for a p-adic counterpart to complex integration used in defining the Abel-Jacobi map, Udi de Shalit pointed out that I was just at the right place… Robert patiently explained the basics of his integration theory and was kind enough to share with me his Minnesota notes on the subject.
Coleman’s integration theory has been further developed since by many people, but to this day his approach remains the most concrete and is being used, and probably will continue to be used, in most of the applications of the theory.
I was fortunate and privileged to be Robert’s high school mathematics teacher. I had him as a student for 3 years from grades 6 through 12. One of the courses I taught him was Abstract Algebra when he was in 11th grade. The text we used was “Topics in Algebra” by Herstein which was quite advanced for high school students. While in the 12th grade, he was student in my mathematics seminar class which was for student who had completed all our our formal courses. The students researched and presented various math topics to each other. That year Robert was a finalist (top 40) in the Westinghouse Science Talent search.
Robert inspired me as a teacher. He loved mathematics and couldn’t get enough of it. When he was applying to colleges, I would say, ” Just put him in a math library for 4 years, and he’ll know more math than than any other undergraduate. Though I taught him more than 42 years ago. I often think of him as the highlight of my 30 years in education.