The Jordan Canonical Form

In my current position as Director of Undergraduate Studies for the Georgia Tech School of Mathematics, I’ve been heavily involved with revamping our linear algebra curriculum. So I’ve spent a lot of time lately reading through various linear algebra books. The goal of this post is to give a self-contained proof of the existence and uniqueness of the Jordan Canonical Form which is somewhat different from the ‘usual’ proofs one finds in textbooks. I’m not claiming any novelty — I’m sure this approach has been discovered before — but I don’t know a good reference so I thought I’d record the details here.

The proof I give here does not use properties of polynomials (e.g. the Chinese Remainder Theorem), nor does it rely on the classification of finitely generated modules over a PID, so it might be of some pedagogical interest. The proof I give for the Generalized Eigenvector Decomposition is based on an auxiliary result — the Fitting Decomposition — which in my opinion ought to be better known. The proof I give of the structure theorem for nilpotent operators comes from these lecture notes of Curt McMullen (Theorem 5.19). It is particularly concise compared to some other arguments I’ve seen.

Jordan Canonical Form

Recall that an elementary Jordan block $J_m(\lambda)$ is an $m \times m$ matrix of the following form (illustrated with $m=5$ ):A matrix is in Jordan Canonical Form if it is a block sum of elementary Jordan blocks, for example:

The theorem we wish to prove is that, over an algebraically closed field $F$ , every $n \times n$ matrix is similar to a matrix in Jordan Canonical Form, and the latter is unique up to rearranging the elementary Jordan blocks. Thus two $n \times n$ matrices are similar over $F$ if and only if they have the same Jordan Canonical Forms (up to rearranging the blocks). More canonically, we want to show that if $V$ is a finite-dimensional vector space over $F$ and $T : V \to V$ is a linear operator, then $V$ is direct sum of $T$ -invariant subspaces $V_i$ such that the matrix of $T$ restricted to $V_i$ (with respect to some ordered basis $B_i$ ) is an elementary Jordan block. The latter condition means that there is $\lambda \in F$ and a vector $v \in V_i$ with $(T-\lambda I)^m v = 0$ such that $v, (T-\lambda I)v, \ldots, (T-\lambda I)^{m-1} v$ is a basis for $V_i$ .

Fitting Decomposition

Let ${V}$ be a finite dimensional vector space over a field ${F}$ , and let ${T : V \rightarrow V}$ be a linear endomorphism.

Theorem 1 (Fitting Decomposition): There is a unique direct sum decomposition ${V = V_n \oplus V_i}$ with the following properties:
1. (1) Both ${V_n}$ and ${V_i}$ are ${T}$ -invariant.
2. (2) ${T}$ is nilpotent on ${V_n}$ .
3. (3) ${T}$ is invertible on ${V_i}$ .

Proof: The chain ${{\rm Ker}(T) \subseteq {\rm Ker}(T^2) \subseteq \cdots}$ must stabilize to a ${T}$ -invariant subspace ${V_n}$ and the chain ${{\rm Im}(T) \supseteq {\rm Im}(T^2) \supseteq \cdots}$ must stabilize to a ${T}$ -invariant subspace ${V_i}$ .
We claim that ${T}$ is nilpotent on ${V_n}$ and ${T}$ is invertible on ${V_i}$ . Indeed, it is easy to see that ${T(V_i) = V_i}$ , which implies that ${T}$ is invertible on ${V_i}$ by the Rank-Nullity Theorem, and ${V_n = {\rm Ker}(T^m)}$ for some ${m \geq 1}$ and thus ${T}$ is nilpotent on ${V_n}$ .

Next, we claim that ${V = V_n \oplus V_i}$ . It is clear from what we have already shown that ${V_n \cap V_i = (0)}$ . So it suffices to show that every ${v \in V}$ can be written as ${v_n + v_i}$ with ${v_n \in V_n}$ and ${v_i \in V_i}$ . Without loss of generality (replacing ${m}$ by a larger integer if necessary), we may assume that ${V_n = {\rm Ker}(T^m)}$ and ${V_i = T^m(V)}$ for the same ${m}$ . Since ${{\rm Im}(T^{2m}) = {\rm Im}(T^m)}$ , we have ${T^m(v) = T^{2m}(w)}$ for some ${w \in V}$ . Then ${T^m(v - T^{m}(w)) = T^m(v) - T^{2m}(w) = 0}$ so ${v_n := v - T^m(w) \in V_n}$ . Setting ${v_i := T^m(w) \in V_i}$ gives the desired decomposition of ${v}$ .

Finally, we show that the decomposition ${V = V_n \oplus V_i}$ is unique. Suppose ${V = A \oplus B}$ with ${T}$ nilpotent on ${A}$ and invertible on ${B}$ . Then ${A \subseteq {\rm Ker}(T^k)}$ for some positive integer ${k}$ , and ${B \subseteq {\rm Im}(T^k)}$ for every positive integer ${k}$ . Thus ${A \subseteq V_n}$ and ${B \subseteq V_i}$ . By dimension considerations, we must have ${A=V_n}$ and ${B=V_i}$ . ${\blacksquare}$

Generalized Eigenvector Decomposition

Let ${\lambda}$ be an eigenvalue of ${T}$ . A generalized eigenvector for ${T}$ with eigenvalue ${\lambda}$ is a vector ${v \in V}$ such that ${(T - \lambda I)^k v = 0}$ for some positive integer ${k}$ . The generalized eigenspace ${E_\lambda(T)}$ is the subspace of ${V}$ consisting of all generalized eigenvectors for ${T}$ with eigenvalue ${\lambda}$ . Note that ${E_\lambda(T)}$ can also be characterized as the nilpotent part of the Fitting Decomposition of ${T - \lambda I}$ .

Lemma: If ${N}$ is nilpotent on ${V}$ and ${\mu \in F}$ is non-zero, then ${N - \mu I}$ is invertible on ${V}$ .

Proof: Suppose ${v \in {\rm ker}(N - \mu I)}$ . Then ${Nv = \mu v}$ , so ${N^k v = \mu^k v}$ for all positive integers ${k}$ . Choosing ${k}$ large enough so that ${N^k = 0}$ , we have ${\mu^k v = 0}$ which implies that ${v = 0}$ . ${\blacksquare}$

Theorem 2 (Generalized Eigenvector Decomposition): Assume that every eigenvalue of ${T}$ (over some extension of ${F}$ ) is defined over ${F}$ , and let ${\lambda_1,\ldots,\lambda_m}$ be the distinct eigenvalues of ${T}$ . Then
$\displaystyle V = \oplus_{j=1}^m E_{\lambda_j}(T).$

Proof: Let $\lambda_1 \in F$ be an eigenvalue of $T$ , and let ${V = V_n \oplus V_i}$ be the Fitting Decomposition of ${V}$ relative to ${T - \lambda_1 I}$ . Since ${V_n = E_{\lambda_1}(T) \neq (0)}$ , it follows by induction that ${V_i}$ is a direct sum of generalized eigenspaces for ${T}$ . We claim that the generalized eigenspaces of ${T|_{V_i}}$ are precisely the ${E_{\lambda_j}(T)}$ for ${j > 1}$ . Given this claim, the Theorem follows immediately. To prove the claim, we make the following observations:

(1) Every eigenvalue of ${T}$ restricted to ${V_i}$ is equal to ${\lambda_j}$ for some ${j > 1}$ .
This follows from the easily verified facts that every eigenvalue of ${T|_{V_i}}$ is also an eigenvalue of ${T}$ , and ${\lambda_1}$ is not an eigenvalue of ${T|_{V_i}}$ .

(2) For ${j > 1}$ , the generalized eigenspace of ${T}$ with respect to ${\lambda_j}$ equals the generalized eigenspace of ${T|_{V_i}}$ with respect to ${\lambda_j}$ .
Any generalized eigenvector for ${T|_{V_i}}$ is automatically a generalized eigenvector for ${T}$ . Conversely, if ${E = E_{\lambda_j}(T)}$ for some ${j > 1}$ , then the restriction of ${T - \lambda_j I}$ to ${E}$ is nilpotent, so by the Lemma the restriction of ${T - \lambda_1 I = (T - \lambda_j I) - (\lambda_1 - \lambda_j) I}$ to ${E}$ is invertible. It follows that ${E \subset {\rm Im \;} (T - \lambda_1 I)^k}$ for all positive integers ${k}$ , so ${E \subset V_i}$ by the proof of Theorem 1. ${\blacksquare}$

Nilpotent Operators and Cyclic Vectors

A subspace ${W}$ of ${V}$ is called cyclic with respect to ${T}$ if there is a vector ${w \in W}$ and a positive integer ${m}$ such that ${w,Tw,\ldots,T^{m-1}w}$ is a basis for ${W}$ .

Theorem 3 (Cyclic Decomposition for Nilpotent Operators): If ${T}$ is nilpotent on ${V}$ , then ${V}$ is a direct sum of cyclic subspaces for ${T}$ .

Proof: Suppose that ${T}$ is nilpotent of exponent ${m}$ , i.e., ${T^m = 0}$ on ${V}$ but ${T^{m-1} \neq 0}$ . Choose ${v \in V}$ with ${v \not\in {\rm ker}(T^{m-1})}$ and let ${A}$ be the ${T}$ -invariant subspace of ${V}$ spanned by ${v, Tv, \ldots, T^{m-1} v}$ . We claim that ${A}$ has a ${T}$ -invariant complement, i.e., there exists a ${T}$ -invariant subspace ${B}$ of ${V}$ with ${V = A \oplus B}$ . Assuming the claim, it follows by induction that ${B}$ is a direct sum of cyclic subspaces for ${T}$ and the Theorem is proved.

To prove the claim, let ${A_0 = A}$ and let ${A_1 = T(A_0)}$ . Note that the restriction of ${T}$ to ${{\rm Im}(T)}$ has exponent ${m-1}$ , so by induction there is a ${T}$ -invariant decomposition ${{\rm Im}(T) = A_1 \oplus B_1}$ . Let ${B_0 = T^{-1}(B_1)}$ . We make the following two observations:

(1) ${A_0 + B_0 = V.}$
To see this, note that if ${v \in V}$ we have ${Tv = a_1 + b_1 \in A_1 \oplus B_1}$ and ${a_1 = T(a_0)}$ for some ${a_0 \in A_0}$ . As ${T(v-a_0) = b_1 \in B_1}$ , we have ${v-a_0 \in B_0}$ .

(2) ${A_0 \cap B_1 = (0).}$
Indeed, ${B_1 \subseteq {\rm Im}(T)}$ implies that ${A_0 \cap B_1 = A_1 \cap B_1 = (0)}$ .

By (1) and (2), there exists a subspace ${B}$ with ${B_1 \subseteq B \subseteq B_0}$ such that ${V = A_0 \oplus B}$ . (Augment a basis for ${A_0 \oplus B_1}$ to a basis of ${V}$ using vectors in ${B_0}$ .) Since ${T(B) \subseteq T(B_0) \subseteq B_1 \subseteq B}$ , we can take ${B}$ to be the desired ${T}$ -invariant complement. ${\blacksquare}$

Dénouement

Combining Theorems 2 and 3, we deduce:

Theorem 4 (Jordan Canonical Form): There is an ordered basis ${B}$ for ${V}$ such that the matrix of ${T}$ with respect to ${B}$ is a block sum of elementary ${k \times k}$ Jordan matrices ${J_k(\lambda)}$ . The number of Jordan blocks with a given size and given eigenvalue is independent of the choice of ${B}$ .

Proof: By Theorem 2, ${V}$ is a direct sum of generalized eigenspaces ${E_{\lambda}(T)}$ for ${T}$ , and by Theorem 3 each ${E_\lambda(T)}$ is a direct sum of cyclic subspaces for ${T - \lambda I}$ . Amalgamating the various ordered bases coming from these cyclic subspsaces gives an ordered basis ${B}$ for ${V}$ with the required property. The uniqueness part follows from the easily verified observation that the number of Jordan blocks of size at least ${k}$ and eigenvalue ${\lambda}$ is equal to ${{\rm dim \;} {\rm ker} (T-\lambda I)^k - {\rm dim \;}{\rm ker} (T - \lambda I)^{k-1}}$ . ${\blacksquare}$

Corollary: Assume that ${F}$ is algebraically closed. Then two ${n \times n}$ matrices ${A}$ and ${B}$ are similar over ${F}$ if and only if they have the same eigenvalues (say ${\lambda_1,\ldots,\lambda_m}$ ) and for all ${1 \leq i \leq m}$ and ${1 \leq k \leq n}$ we have ${{\rm dim \;}{\rm ker} (A-\lambda_i I)^k = {\rm dim \;} {\rm ker} (B-\lambda_i I)^k}$ .

5 thoughts on “The Jordan Canonical Form”

Eric Katz says:

August 4, 2015 at 10:07 pm

Very nice. At the risk of being pointlessly abstract, to get a decomposition independent of any choices, one can use the Jacobson-Morosov structure theorem for nilpotent operators. This is just the classical name for the Lefschetz-type filtration used for monodromy.

David Speyer says:

August 21, 2015 at 2:14 pm

The argument in Theorem 3 is very nice. I remember finding this surprisingly hard to find a good elementary proof for when I did it last year; I think I’ll steal your approach next time. It is worth pointing out that the reason you know $A_0 \cap T(V) = A_1$ is because, otherwise, $T$ would have exponent larger than $m$ .

- Matt Baker says:
  
  August 21, 2015 at 4:04 pm
  
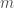  Thanks, David — I’ve incorporated your suggestion to explain in more detail why $A_0 \cap T(V) = A_1$ .
  
Small remark says:

November 12, 2015 at 2:34 pm

Nice article. Just a small remark: it’s clear that V_i and V_n are im T^p and ker T^p, respectively, with the same index p. So, by the rank-nullity theorem, they must have complementary dimension. Consequently, once you’ve (easily) shown that V_n ∩ V_i is trivial, you have V = V_n ⊕ V_i for free.

- Matt Baker says:
  
  November 12, 2015 at 2:40 pm
  
  Good point, thanks!