In January 2016, my colleague Josephine Yu and I are organizing a workshop called Hodge Theory in Combinatorics. The goal of the workshop is to present the recent proof of a 50-year-old conjecture of Rota by Karim Adiprasito, June Huh, and Eric Katz. In this post, I want to explain what the conjecture says and give a brief outline of its marvelous proof. I will follow rather closely this paper by Adiprasito-Huh-Katz (henceforth referred to as [AHK]) as well as these slides from a talk by June Huh.
Chromatic polynomial
If is a finite graph, a proper coloring of
with
colors is a function
from the vertices of
to
such that if
are adjacent then
. Whitney proved in 1932 that the function
giving the number of proper colorings of
with
colors is a polynomial in
, called the chromatic polynomial of
. (The celebrated four-color theorem asserts that if
is planar then
.)
 Read conjectured in 1968 that for any graph
Read conjectured in 1968 that for any graph , the coefficients of
form a log-concave sequence, i.e.,
for all
. Read’s conjecture was proved by June Huh in a 2012 JAMS paper using methods from algebraic geometry.
A recursive algorithm for computing makes use of the observation that
satisfies the deletion-contraction identity
where
denotes
with
deleted and
denotes
with
contracted. This identity also yields a simple inductive proof that
is indeed a polynomial.
Independent sets of vectors
If is a vector space over an arbitrary field and
is a finite set of vectors in
, define
to be the number of independent subsets of
of size
. For example, if
is the set of all non-zero vectors in
(corresponding to the Fano matroid), we have
Welsh conjectured in 1969 that
is always a log-concave sequence. Welsh’s conjecture was proved by Lenz, who reduced it to the main theorem in the 2012 Mathematische Annalen paper of Huh and Katz, which itself built on the prior work of Huh.
Matroids
Gian-Carlo Rota noticed that there is a common generalization,in the context of matroids,of the chromatic polynomial of a graph and (a close cousin to) the sequence above. I gave an introduction to matroids in this blog post, characterizing them in terms of independent subsets and circuits. For the purposes of the present exposition, it will be convenient to present the following two alternative axiomatizations in terms of rank functions and flats.
Axiomatization in terms of rank functions
A matroid is a finite set
together with a function
from the collection
of subsets of
to the non-negative integers, called the rank function of
, such that:
• (R1) If then
.
• (R2) If and
, then
.
• (R3) (Submodularity axiom) If then
.
Axiomatization in terms of flats
A matroid is a finite set
together with a collection
of subsets of
, called flats of
, such that:
• (F1) .
• (F2) If then
.
• (F3) (Covering axiom) If and
, there is a unique minimal (with respect to inclusion)
containing
with
.
The connection with the independence axioms discussed in my earlier blog post is (briefly) as follows. The rank of a subset of
is the cardinality of the largest independent subset of
; in particular,
is independent if and only if
. A subset
of
is a flat of
if and only if
for every
.
The rank of is defined to be
, i.e., the rank of the largest maximal independent set in
. The corank of a subset
of
is
.
Characteristic polynomial of a matroid
Generalizing the construction of the chromatic polynomial of a graph, Rota defined the characteristic polynomial of a matroid as
An equivalent but more useful definition is
where is the Möbius function of the poset of flats of
. (Alternatively, one can define
recursively using the deletion-contraction identity
)
Rota made the following conjecture in 1964:
Conjecture: The absolute values of the coefficients of
form a log-concave sequence.
This is the main theorem which Adiprasito, Huh, and Katz prove in their paper. It implies the conjectures of Read and Welsh mentioned above, but is significantly more general because it applies to all matroids and not just representable ones. (June Huh likes to point out that, at least heuristically, one expects that 100% of all matroids are not representable.)
The Chow ring of a matroid
We briefly outline the strategy used by Adiprasito, Huh, and Katz in their proof of Rota’s conjecture. The first step is to define a Chow ring associated to an arbitrary matroid
. The definition is due to Feichtner and Yuzvinsky, who noted that when
is realizable over
the ring
coincides with the usual Chow ring of the de Concini-Procesi “wonderful compactification”
of the hyperplane arrangement complement associated to
. Although the definition of
is purely combinatorial and does not require any notions from algebraic geometry, it would presumably be rather hard to motivate the following definition without knowing something about the relevant geometric background.
Let be the poset of non-empty proper flats of
. The graded ring
is defined as the quotient of the polynomial ring
by the following two kinds of relations. First, one sets
whenever
and
are incomparable in the poset
. Second, one declares that for every
the sum of the
for all
containing
equals the sum of the
for all
containing
.
The generators are viewed as having degree one. If
is the rank of
, there is an isomorphism
determined uniquely by the property that
whenever
is a flag in
.
Connection to Hodge Theory
If is realizable, one can use the so-called “Hodge-Riemann relations” from algebraic geometry, applied to the
-dimensional algebraic variety
whose complex cohomology ring is
to prove Rota’s log-concavity conjecture for
. This is (in retrospect, anyway) the basic idea in the earlier paper of Huh and Katz.
We now quote from the introduction to [AHK]:
While the Chow ring ofcould be defined for arbitrary
, it was unclear how to formulate and prove the Hodge-Riemann relations… We are nearing a difficult chasm, as there is no reason to expect a working Hodge theory beyond the case of realizable matroids. Nevertheless, there was some evidence on the existence of such a theory for arbitrary matroids.
What the authors of [AHK] do is to formulate a purely combinatorial analogue of the Hard Lefschetz Theorem and Hodge-Riemann relations and prove them for the ring in a purely combinatorial way, making no use of algebraic geometry. The idea is that although the ring
is (presumably) not actually the cohomology ring of a smooth projective variety, from a Hodge-theoretic point of view it behaves as if it were.
In order to formulate precisely the main theorem of [AHK], we need a combinatorial analogue of hyperplane classes, or more generally of ample and nef divisors. The connection goes through strictly submodular functions. A function is called strictly submodular (resp. submodular) if
(resp.
) whenever
are incomparable subsets of
. Such a function
gives rise to an element
The convex cone of all
associated to strictly submodular (resp. submodular) classes is called the ample cone (resp. nef cone). (Actually, the ample cone in [AHK] is a priori larger than what we’ve just defined, but this is irrelevant for the purposes of the present post.)
Ample (resp. nef) classes define strictly convex (resp. convex) piecewise-linear functions on the Bergman fan . I described the Bergman fan in this post in terms of the circuits of
. However, one can also define
using flats; in particular, the cones of
correspond bijectively to flags
of non-empty proper flats of
, where as above
is the rank of
.
The main theorem of [AHK] is the following:
Theorem: Let
be a matroid of rank
, let
be ample, and let
. Then:
• (Poincaré duality) The natural multiplication map gives a perfect pairing
• (Hard Lefschetz Theorem) Multiplication bydetermines an isomorphism
.
• (Hodge-Riemann relations) The natural bilinear formdefined by
is positive definite on the kernel of
(the so-called “primitive classes”).
This is all in very close analogy with analogous results in classical Hodge theory.
To see why the theorem implies Rota’s conjecture, fix . Let
be the sum of
over all
containing
, and let
be the sum of
over all
not containing
. The images of
and
in
do not depend on
, and are denoted by
and
, respectively.
Proposition: For all
,
is equal to the
coefficient of the reduced characteristic polynomial
of
.
Although and
are not ample, they belong to the nef cone and one may view them as a limit of ample classes. This observation, together with the Hodge-Riemann relations, allows one to deduce Rota’s conjecture in a formal way.
Strategy for proving the main theorem
The main work in [AHK] is of course establishing Poincaré duality and especially the Hard Lefschetz Theorem and Hodge-Riemann relations for . The actual proof is much too intricate to describe in this blog post. However, I will try to quickly give an impressionistic view of the argument.
The proof is motivated by Peter McMullen’s observation that one can deduce the g-conjecture for arbitrary simple polytopes to the case of simplicial polytopes using the “flip connectivity” of simplicial polytopes of given dimension.
The key observation in [AHK] motivated by McMullen’s work is that for any two matroids and
of the same rank on the same ground set
, there is a diagram
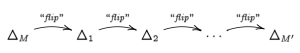
where each matroidal flip preserves the validity of the Hard Lefschetz Theorem and Hodge-Riemann relations. (A subtlety is that the intermediate objects are tropical varieties, i.e., balanced weighted rational polyhedral fans, but not necessarily tropical linear spaces associated to some matroid. So one leaves the world of matroids in the course of the proof, unlike with McMullen’s case of polytopes.) Using this, one reduces Rota’s conjecture to the case of the uniform matroid of rank
on
(whose rank function is given by
for all
), in which case the conjecture can be directly verified “by hand”.
Concluding remarks
1. Every log-concave sequence of positive real numbers is unimodal, i.e., there is a
such that
. In particular, the main theorem of [AHK] implies that the absolute values of the coefficients of the characteristic polynomial of a matroid form a unimodal sequence. See this survey paper by Stanley for many other examples of naturally occurring log-concave and unimodal sequences in combinatorics.
2. The term combinatorial geometry from the title of [AHK] is another name for a simple matroid. (A matroid is called simple if every circuit has at least 3 elements, or equivalently, if the empty set and all singleton subsets of are flats.) Every matroid has a canonical simplification, with the same lattice of flats
, and one can recover a simple matroid uniquely from
. As
can be defined purely in terms of the lattice of flats, one can immediately reduce the main theorem of [AHK] to the case of combinatorial geometries.
3. We have already mentioned that the approach given in [AHK] to proving the Hard Lefschetz Theorem and Hodge-Riemann relations was inspired in large part by the work of Peter McMullen. It is also inspired by the approach to classical Hodge Theory pioneered by de Cataldo and Migliorini.
4. The main theorem of [AHK] is related to the counterexample to Demailly’s strong version of the Hodge conjecture for positive currents given recently by Babaee and Huh. Their counterexample is based on a tropical variety that satisfies Poincaré duality and the Hard Lefschetz Theorem, but not the Hodge-Riemann relations.
5. The proof of the Lefschetz theorem for locally matroidal tropical varieties by Adiprasito and Björner uses a deformation argument similar to the one used in [AHK].


First.
I believe [AHK] use r+1 for the rank of the matroid, rather than r. I was confused for a while by this in your post when trying to understand how there could be a flag of length r ending in a proper flat in the definition of the degree isomorphism of the Chow ring.
You’re right, thanks — I now write r=d+1 and have replaced r by d in several places.
Hi Matt,
One way of expressing log-concavity is that the 2×2 minors of the Toeplitz matrix with the a_i’s down the i-th off-diagonal are non-negative. In the theory of total positivity, one asks that all the minors of such matrices are non-negative. Could it be the case that the log-concave combinatorial sequences you mention above have the property that all these minors are non-negative? Or is this known to be false?
The Hodge Riemann relations we use indeed imply such a statement, but only for rings with 2 generators. Unfortunately we do not have such a sexy statement for matroids in general.
June Huh says: Jim’s condition for the infinite Toeplitz matrix says that the generating polynomial for the sequence mu has only real zeros. Apparently this fails for uniform matroids.
Thanks!
Pingback: 月旦 I | Fight with Infinity
Pingback: Whitney Encounters of the Second Kind | Matt Baker's Math Blog
Pingback: Lorentzian Polynomials II: Applications | Matt Baker's Math Blog
Pingback: Firing games and greedoid languages | Matt Baker's Math Blog
Pingback: A Fields Medal for June Huh! | Matt Baker's Math Blog